Celtic Knotwork Patterns

'Celtic Knotwork Patterns' printed from https://nrich.maths.org/

Show menu

This beautiful decorated letter comes from a book called the Book of Kells. It was drawn by monks hundreds of years ago. If you look carefully, you can see patterns of knots in the decoration. People have found similar patterns in some other books, and carved into stones in Scotland and Ireland.

The idea of this article is to give an introduction to these knotwork patterns and a feel for how they can be drawn. There are some diagrams to show how to draw patterns, and some questions you could think about.

Use the instructions however you like:
You could just print off the line drawings to colour in.
You could use the basic backbones I have drawn and make them into your own patterns.
Or you could draw follow the instructions to draw patterns from scratch, or make up your own.

Drawing a Knot

Let's start by drawing a knot.

Try drawing a knot the way I have shown. Begin by drawing three dots in a triangle. Join them as in the second picture, then change the joining lines to make the knot more the shape you want. Once you have the basic shape, turn the line into a wider string and make it go over, then under, then over, then under the strands it crosses.

Draw the basic shape again. This time, try making two strands follow the line you have drawn. Again, make the strands go alternately over and under the threads they cross.

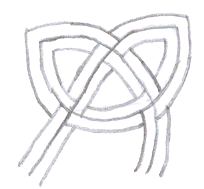
Can you make three strands running alongside each other?

Can you use a piece of string to tie the knot I drew first? Tie some other knots in string and see if you can draw them.

Borders

Now let's try some longer groups of knots.

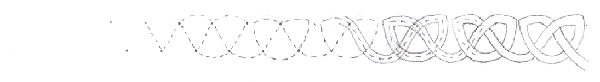
In both pictures, I've started with two rows of dots and joined them in a zig-zag between the rows. Above and below the rows, I've joined each dot to its next-door neighbour.

In the top picture I've just followed the joining lines to make a plait, but in the lower picture I've adjusted them a bit first and made a row of knots.

What if we start with the same two rows of dots but join them in a different way? In this border I've joined the dots to their next-door neighbours at the top of the pattern and to their neighbours-but-one on the bottom.

Try drawing some patterns like this for yourself. You can make your threads thick, thin, doubled ... use your imagination! Experiment by joining the dots in different ways above and below the rows.

How many strands are there in your border?

Try colouring the strands different colours so you can see where they go.

How could you write down the way you joined your sets of dots so that somebody else could draw your border?

You can start with two sets of dots near each other. Then you can join them to each other as well as to themselves.

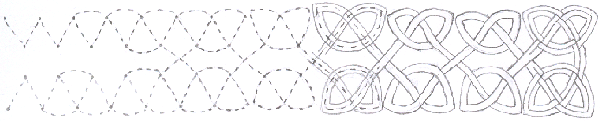
Instead of drawing two rows, draw two circles of dots inside each other. Then your border makes a circle.

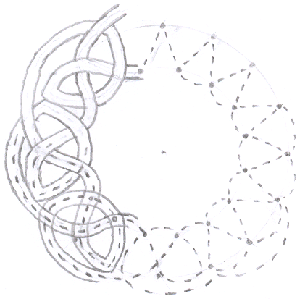
How many dots should you use to make sure your border matches up properly at its ends?

How does the number of dots affect the number of strands in the border?

Can you always draw your strands going alternately over and under the threads they meet or do you sometimes have to cross the same way twice running?

Why?

Panels

Make panels of knotwork by filling in your circular borders, perhaps with more borders, by shrinking the space in the middle or by joining the sides with loops and curls.

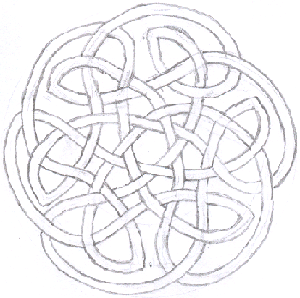
Can you see how I have made this pattern from the one in the picture above it?

Another way to make panels is with grids like these:

Can you see that the grid on the left is made of 5 continuous lines? (Ignore the dotted box round the outside.)

How many lines is the grid on the right made of?

If I am choosing how many dots to use for each side of my grid, is there a rule which I can use to make sure my grid will be just one continuous line?

You can leave your grid as it is, turning the lines into interlacing strands to make your pattern.

Or you can join it up in a different way. In this picture, I started with a grid (the dotted lines), then joined points at the edge (the dashed lines) and joined up some of the lines inside the grid (solid lines). Finally, I turned my lines into interlacing strands.

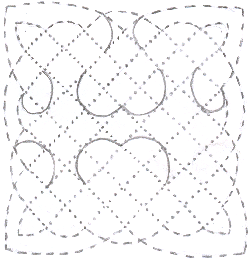
Do these patterns have any lines of symmetry?
Does your answer change if you ignore which strand is on top where two strands cross?
Is there any rotational symmetry?

Colouring and Practising Sheets

I've made some colouring sheets with knotwork patterns on them which you can download and print. There's also a sheet of "skeleton" knots - some basic shapes and borders for you to use to practise interlacing.

References

These methods for designing knotwork came from Celtic Art by George Bain, which contains pages of beautiful, fascinating and meticulously-researched information about Celtic designs and their construction.