Cultivating creativity
Creativity in the mathematics classroom is not just about what pupils do but also what we do as teachers. If we are thinking creatively about the mathematical experiences we offer our pupils we can open up opportunities for them to be creative. In this article, I am going to share some of my thoughts on creative teaching, and how it can encourage creative learners.
This article reflects the belief of colleagues at NRICH that mathematics is about problem solving and problem solving is a creative process. Most students' classroom experiences of mathematics involve studying materials and working through tasks set by their teachers, or being passive observers of mathematics (Boaler 1997) leaving little room for the entrepreneur or creative thinker. Students do not generally expect to be challenged by an unfamiliar situation. When students are placed in problem-solving situations it is nearly always within a context that is very familiar, for example, a problem involving the application of a mathematical concept the students have just been taught. In such situations learners are aware of boundaries, and have been given some clear leads about what knowledge to apply. Such problems often seem closed with very little room to explore and be creative. Problem solving should be about valuing independence and individual ideas, and being given some mathematical space to develop a "habit of mind" that gives opportunities to experience:
"The joy of confronting a novel situation and trying to make sense of it - the joy of banging your head against a mathematical wall, and then discovering that there may be ways of either going around or over that wall"
Page 43 (Olkin and Schoenfeld
1994)
So what things can we do as teachers to offer opportunities for creativity and how can we embed these opportunities into our everyday practice? Three things come to mind:
- how we present content
- how we model good practice
- how we encourage our students to be creative
Presenting content
One concern raised by many teachers, is the need to cover the
content requirements of the national curriculum and exam board
specifications. However, by developing problem-solving skills and
using problems to explore aspects of mathematics, learners can feel
empowered to "think for themselves" and, as a result, become more
confident when tackling standard questions. Giving problem solving
a much higher profile in our classrooms might feel like a high-risk
strategy to many of us, but there are ways of giving students room
to explore and still covering content.
One way in which NRICH is trying to support this is by
developing interactive environments with guidance for teachers and
students concerning the potential of the interactivity to support
aspects of the curriculum.
The interactive "Tilted Squares", published in September 2004,
is based on the ability to create tilted squares on a coordinate
grid and to use this to investigate the area of squares with
different tilts as shown in the diagram.
Image
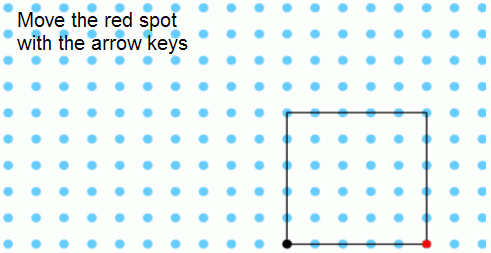
Some suggested questions on the site include:
What areas are possible?
What areas are impossible?
Why?
What observations, thoughts and conclusions can you
offer?
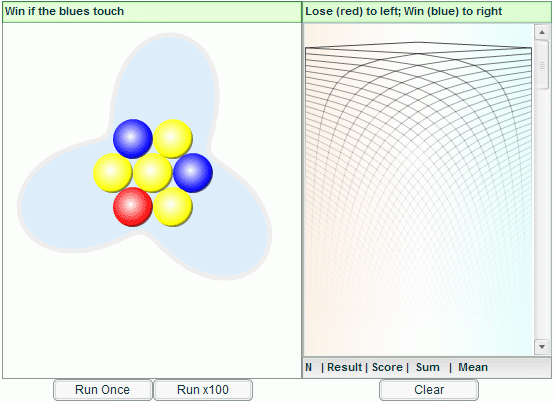
In the case of Probability, several environments were
published in November 2005, that aim to focus attention on
justifying experimental probabilities. The picture belowis from the
problem "Two's Company" which poses a question:
"7 balls are shaken in a container. You win if the two blue
balls touch. What is the probability of winning"?
Image
Such environments enable students to explore and work from
their own level of understanding, building on this towards new
understandings. For example, in the case of Tilted Squares,
students have worked at a range of levels:
- some have made progress in understanding that squares do not have to be constructed with sides parallel to the edges of the paper they are drawn on;
- some have begun to identify relationships between the amount of tilt and the areas of squares;
- others have been able to generalise and offer a justification of Pythagoras' Theorem for right-angled triangles with two short sides of integer length.
It is also possible to base work on interactive environments
which are not ICT based. A wealth of NRICH activities based on
plastic Geoboards, number cards or plastic cubes, for example, give
students room to manipulate objects as they think through
ideas.
Modelling
As teachers, we rarely model problem solving in the
mathematics classroom. After all, we usually arrive at the lesson
knowing what we want to teach, having a very good idea of what
questions we are likely to be asked and being well prepared to
answer them without any indication of the work or thought processes
we may have gone through before entering the room. How can we begin
to share with students the fact that we can also struggle with
mathematics and that this is the "normal" state of affairs when
meeting something new? What is important is that at any point of
being STUCK we acknowledge that we are stuck, and share our thought
processes as we start putting our creative juices to work (Mason,
Burton et al. 1982). At these points we should not be afraid to
experiment and try ideas out - this is a common strategy we can all
use. Perhaps is a good way to try this out is to walk into the
classroom with a problem we have found in an old text book or
mathematical activity book, such as books by Martin Gardner
(Gardner 1965), and say "Let's look at this together" -and then
spend time thinking out loud. I am not denying that this feels
threatening, but we need to show the students that this is a fairly
normal state of affairs by sharing such an experience with them
from time to time. Allowing students to watch us struggle whilst
describing what we are doing as problem solvers is a powerful
model.
Posing problems
Mathematics is as much about posing problems as problem
solving, noticing within a situation that there is a question
waiting to be asked. At this point, the creativity is in noticing
there is something to be investigated. When setting up situations
in the classroom we should make an effort to choose contexts that
offer students opportunities to pose their own problems. Resources
such as the interactive environments I have described above are
excellent for this purpose.
Questioning
A powerful tool in supporting students as independent,
creative thinkers is the use of questioning. Using effective
questioning is not always easy, especially when many of us are in
the habit of questioning with a particular answer in mind, closing
down opportunities for the mathematical entrepreneur in our class
to suggest other ideas. There is much complexity in both the style
and purpose of questions we ask. In their book, Questions and
Prompts for Mathematical Thinking (1998), Anne Watson and John
Mason help to make sense of some of that complexity and give
concrete examples of how we can encourage students' mathematical
thinking . If questions are used to elicit individual ideas, then
the classroom also needs to value difference and work as a
community learning from that diversity and creativity. The
unexpected answer can be used as a springboard for development,
rather than acknowledged but left hanging, simply because it is
unexpected. Different approaches to a problem which can emerge as a
result of our questioning not only offer opportunities for
discussing mathematics and considering issues such as the elegance
of a solution but also tell us a lot about what our students
understand and what further support they need. For example,
students can be very ingenious in avoiding the use of standard
algebraic techniques if they are not confident - this not only
tells us that they need support with a particular range of
techniques but, more importantly, it tells us what they are
confident with and how they can use their knowledge
creatively.
Solutions
As soon as a problem is posed we may wish to find a solution
-often there is more than one solution and usually there is more
than one route to it. So, starting from that point we should be
encouraging creativity by acknowledging different solutions,
evaluating them for elegance and efficiency. NRICH publishes
students' solutions to encourage clear explanations and to enable
comparison and evaluation different approaches.
Some time ago I was at a session run by a colleague who set a
problem to a group of students he had not met before, but who were
embarking on their first session of a long course on problem
solving. One of the problems he set, Sums of Pairs (published in
December 2002) was:
"Jo has three numbers which she adds together in pairs. When
she does this she has three different totals:
11, 17 and 22
What are the three numbers
Jo had to start with ?"
In the session the students worked in small groups adopting
different approaches to the solution:
- some students used an algebraic approach (calling the original three numbers a, b and c);
- others used trial and improvement: one of these groups starting by saying that the smallest number has to be 5 or less in order to make a total of 11...;
- another group of students found a solution almost "by accident" and at this point they were given a similar problem to encourage them to explore a generalisable method.
All three methods were identified by my colleague, who
encouraged the students to discuss approaches they found most
accessible, repeatable and efficient. This exploration of solutions
indicated that value was being placed on individuality, as
differences were valued and formed part of the learning process. It
was the means by which the learners made their journeys towards a
solution rather than the solution itself which formed the focus of
the lesson. Whilst encouraging individuality, my colleague also
gave direction after waiting to see where the students were. He
valued what the students said but it required students that felt
confident enough to communicate with their peers. The teachers
present at the session reflected on the role of students as
learners in an active sense; they talked of their work in terms of
engagement and communication. Students engaged in their own
learning by attending to the ideas of others, by experimenting,
exploring and being critical.
In essence we as teachers play a vital part in creating an
environment in which creativity and individuality is valued and
utilised.
The curriculum
So, how does this affect what we teach and how we can support
teaching it? At NRICH we try to offer problems that give scope for
creativity and environments designed to encourage students to pose
their own problems. But how can these be used in practice? Setting
challenging problems that encourage students to be creative and to
discuss and evaluate their mathematics is one thing, but building a
programme of activities into a scheme of work over a longer period
of time needs planning and a rationale for what we hope to achieve.
On one level being mathematical is about being creative with the
tools we have available to us. We do not need to be engaging in
high level mathematics in order to be creative -what we need to be
able to do is recognise what mathematics we might use and then
apply it in creative ways. On another level, being creative is also
about evaluating other people's approaches in terms of their
efficiency. But, there is a level of creativity that we as teachers
need to bring to bear in terms of the diet we give to our students
-even caviar and champagne can be boring if that is what you have
every day!
By implication, students can only be creative problem solvers
if they are given the freedom to be creative. An obvious way to
achieve this is through the use of material that opens up
opportunities to explore and discover, and make sense of,
mathematics. One way of achieving this is by looking at aspects of
the curriculum and thinking less about the content and more about
experiences.
Questioning and encouraging students to think for themselves
and share their understandings are important aspects of any
curriculum and a focus on problem solving and posing offers a way
forward.
So, what are the key features of a problem-solving curriculum?
One where students and teachers:
- engage in problem solving and problem posing;
- have access to experimental opportunities (environments) to explore which have the potential to lead to particular mathematical ideas;
- are mathematising (identifying the mathematics in situations);
- make connections with other mathematical experiences;
- engage in and examine other people's mathematics;
- are not constrained by the content of the previous lessons but supported by them;
- value individuality and multiple outcomes;
- value creative representation of findings.
Concluding remarks
Mathematics is a creative subject and we as teachers need to
be prepared to present it in more varied ways, including being
prepared to "let go" and give our students room to explore. In
doing this we are not only allowing them access to what mathematics
is really about -posing and solving problems - but also offering
situations in which students can reveal their strengths and
highlight areas where they need greater support. This is what we at
NRICH aim to support teachers and learners in doing.
References
- Boaler, J. (1997). Experiencing School Mathematics . Buckingham, Open University Press.
- Gardner, M. (1965). Mathematical Puzzles and Diversions , Penguin.
- Mason, J., L. Burton, et al. (1982). Thinking Mathematically , Prentice Hall.
- Olkin, I. and A. Schoenfeld, H. (1994). A Discussion of Bruce Reznick's Chapter [Some Thoughts on Writing for the Putnam]. Mathematical Thinking and Problem Solving Schoenfeld, A, H. Hillside NJ, Lawrence Erlbaum: 39-51.
- Piggott, J. S. and E. M. Pumfrey (2005). Mathematics Trails - Generalising , CUP.
- Watson, A. and J. Mason (1998). Questions and Prompts for Mathematical Thinking , Association of Teachers of Mathematics.
