Copyright © University of Cambridge. All rights reserved.
Mobile Numbers

So many of us are using mobile phones and you have numbers like that one above. (+44 instead of the first 0 when you are phoning the UK from abroad.)
Some numbers are easy to remember!
Some seem to have a pattern about them!
Let's have a look at how we might invent some mobile phone numbers that would be easy to remember.
We could start with a number and have a simple rule that gives us the next number, like starting with 3 and adding 2 each time:
1 3 5 7 etc.
and when the number is bigger than 9 we could just write down the units figure. For example:
1 3 5 7 9 1 3 5 7 9 1 3
Here are some suggestions about how you could go on with this idea:
but we could start with any of the numbers, 1 ... 9.
A. Try adding on 2 each time as in the example above, but starting with any number, 1 ... 9 and see what you get.
What do you notice? Talk to someone else about your ideas!
Try adding on 3 each time instead - starting with 1 then 2 then 3 ...
(For example starting with 5 it would be 5 8 1 4 7 0 3 6 9 2 5 8.)
B. We could try adding on a 4 each time, and so on.
C. We could multiply instead. Suppose we've done multiplying by 2, 3, 4 and 5 and we come to 6. Starting with
1 we'd have:1 6 6 6 6 6 6 6 6 6 6 6
2 we'd have: 2 2 2 2 2 2 2 2 2 2 2 2
3 we'd have: 3 8 8 8 8 8 8 8 8 8 8 8
So carry on!
Again, what do you notice? Have a chat to someone else about it.
D. We could use two rules, but only changing one at a time - I'll show you what I mean. Suppose we use "add ... then multiply by 9" and have "adding 1" as a first idea.
Starting with
1 we'd have : 1 8 1 8 1 8 1 8 1 8 1 8
2 we'd have : 2 7 2 7 2 7 2 7 2 7 2 7
3 we'd have : 3 6 3 6 3 6 3 6 3 6 3 6
... so carry on.
But we could add 2 or 3 or 4 ... each time instead and explore the nine patterns each time.
So, for example, adding on 5 then multiplying by 9 we get the following 9 patterns
1 4 1 4 1 4 1 4 1 4 1 4
2 3 2 3 2 3 2 3 2 3 2 3
3 2 3 2 3 2 3 2 3 2 3 2
4 1 4 1 4 1 4 1 4 1 4 1
5 0 5 0 5 0 5 0 5 0 5 0
6 9 6 9 6 9 6 9 6 9 6 9
7 8 7 8 7 8 7 8 7 8 7 8
8 7 8 7 8 7 8 7 8 7 8 7
9 6 9 6 9 6 9 6 9 6 9 6
E. You may be getting the idea. You could use any combination of rules.
What about using division?
Those of you with spreadsheet skills could use these ideas to explore quite far!
It is through investigations like this that you have opportunities of exploring and extending knowledge of many different aspects of number work. In this activity there are opportunities to work on repeat patterns, reflective patterns, number patterns related to tables, addition, subtraction, multiplication, setting further challenges, systematic working and perseverance.
Many of the patterns that are generated almost duplicate others. For example if the rule is to multiply by 3, this is what you get starting with each digit in turn:
1 3 9 7 1 3 9 7 1 3 9 7
2 6 8 4 2 6 8 4 2 6 8 4
3 9 7 1 3 9 7 1 3 9 7 1
4 2 6 8 4 2 6 8 4 2 6 8
5 5 5 5 5 5 5 5 5 5 5 5
6 8 4 2 6 8 4 2 6 8 4 2
7 1 3 9 7 1 3 9 7 1 3 9
8 4 2 6 8 4 2 6 8 4 2 6
9 7 1 3 9 7 1 3 9 7 1 3
so pupils need to decide whether to explore all or just the three that are substantially different.
Here are some good ones to explore if you and the pupils are short of ideas.
A. Here are just the first three (out of nine) parts of three ideas that are good for exploring odds and evens as well as interesting repeats. The first is add ... then multiply by 2:
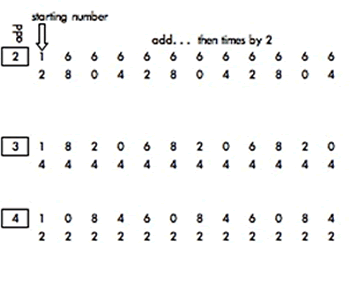
Or add ... then multiply by 3:

Or add ... then multiply by 7:

B. Here are the four parts that lend themselves to exploring carefully what is happening in multiplying by 6 and multiplying by 9 in each of the three rules, then making a comparison.
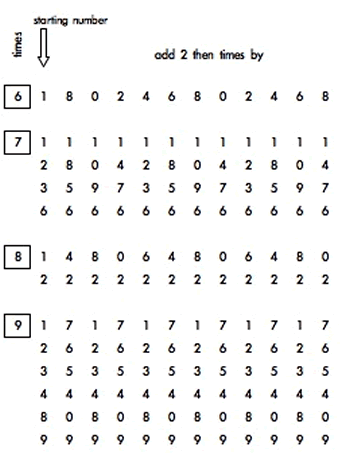


C. And a really simple one that comes from a rule that looks as if it might be harder:
D. Another suggestion is using three rules, for example multiplying by the numbers 1, 2, ... 9 then an operation, then multiplying again.













