Exploring the Challenge of Online Mediation

'Exploring the Challenge of Online Mediation' printed from https://nrich.maths.org/

Show menu

This paper will report on students' responses to a mathematical problem from the NRICH website. In particular, we were interested in students' responses to a question that provided an unusual challenge. Their responses have informed our identification of a range of students' attitudes which can be placed along a continuum. We have used the findings to suggest mediation strategies that could be offered on a website to meet the needs of learners throughout the continuum. These mediation strategies take into account the strategies used by teachers in classrooms.

The NRICH Website

NRICH (www.nrich.maths.org.uk) is a web based resource that aims to provide mathematical enrichment for all people from the age of 5 onwards. It offers problems that are more interesting and challenging than those found in standard textbooks in the hope that students and teachers will appreciate the contribution they can make to mathematical thinking and understanding. Recent research has recognized the deficiencies of a mathematics curriculum that is mainly based on skills and procedures and advocates a curriculum that offers students more opportunities to be mathematical and that respects them as responsible learners of mathematics (Ahmed 1987) (Boaler 1997) (Jaworski 1994) (Askew, Brown et al. 1997) (Watson, Geest et al. 2002).

Most people's exposure to mathematics is based on their experiences at school, mainly through textbooks (Galbraith and Chant 1990). NRICH is offering something different: most of the mathematics problems on the website cannot be easily pigeon holed into a chapter in a textbook but require students to use a range of unspecified skills. Textbooks tend to suggest there is a best way of doing things and promote a limited number of tried and tested algorithms. NRICH problems, in contrast, can often be solved by non-standard methods and in a variety of ways.

What is the impact of this on the people who use NRICH? If they come with the "school maths" mindset, where they expect to see a problem and know what to do, they may give up when they do not know how to proceed. In school the right strategy has generally been modelled for them in advance whereas the website problems assume users will take time to think for themselves. In many classrooms most students know what to do because they are following a procedure for which they have been trained; there is the expectation that the majority of students will follow that procedure successfully. In these classrooms there is often a lot of mediation at the start of lessons in which teachers prepare students for what they are about to do and on-going mediation that offers clarification and reminders.

These features of classroom life are not available to students tackling problems on the NRICH website. In this online environment

users are not told what mathematics to use
users may be working on their own without support from teacher or peers.

Students who have been brought up in the stereotypical classroom culture described above will be in an unfamiliar situation. This paper explores how mediation could be offered on a website like NRICH without diminishing the challenge to users to think mathematically.

Thinking mathematically usually requires students to search for possible methods of attack and to realise the importance of making conjectures and generalisations. These conjectures may be tentative and provisional and are open to challenge from others but they can be developed into results which can eventually be justified and proved (Mason, Burton et al. 1985) (De Geest, Watson et al. 2003). There is value in allowing students to pursue their own individual lines of investigation regardless of the most efficient way of reaching the solution to a problem. However, we must acknowledge that this may be a very uncomfortable experience for them (De Geest, Watson et al. 2003) (Holt 1964).

Mediation

It is necessary to consider the nature of mediation in teaching and learning contexts. In classrooms, teachers are engaged in mediating between students and the mathematics: they check that the students have read the question and that they understand the task; they suggest a first (or second or third...) move; they demonstrate connections with previous work or experiences; they simplify the task or demonstrate an analogous task; they ask questions to encourage students to pursue fruitful avenues of enquiry. With different children and different tasks, a very varied and rich range of possible options is open to teachers.

All this is highly dependent on teachers' professional judgements about appropriate actions in different contexts. It involves a sensitive reading of the situation and may be adapted or altered in subtle ways to match the perceived needs of different students. Barbara Jaworski (Jaworski 1994) has identified a teaching triad containing three elements of teachers' professional practice: management of learning, sensitivity to students and mathematical challenge. This triad will inform the analysis of the mediation that can be offered on a website like NRICH.

The Study

To get some sense of what mediation might help, we asked 70 students aged between ten and eleven to try the "Make 37" problem and then administered a questionnaire that asked them about the experience of tackling this non-standard problem. The questionnaire enabled us to collect a large number of responses immediately after the students had attempted the problem; this ensured that the experience was easily recollected. We specifically asked them about what they liked and disliked and for their recommendations for helpful hints. This generated qualitative data that we analysed using grounded theory (Silverman 2001) (Strauss and Corbin 1990)

Here is the "Make 37" problem that first appeared on the NRICH website in 2003 (http://nrich.maths.org/public/viewer.php?obj_id=1885 ).

Make 37

Four bags contain a large number of 1s, 3s, 5s and 7s.

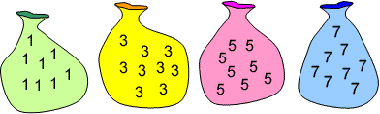
Pick any ten numbers from the bags above so that their total is 37.

Superficially the problem seems little different from a standard textbook task asking students to make numbers from smaller numbers and giving them practice in adding a series of small numbers together. However it turns out to be rather different from that and after a little investigation and thought students begin to realise that the problem might not have a solution after all, and some eventually decide that it is impossible. As a consequence, the solution to the problem requires students to provide a convincing argument that shows why it is impossible.

The Findings: Two Extremes along aContinuum

We have selected quotes from students that can be positioned on the extremes of a continuum, from very positive to very negative reactions to the problem.. Initially we would like to consider the comments made by students who appreciated the experience of working on the problem.

Students appreciated the chance to work on something different:

I liked it because the problem made me think harder than I have in a Maths lesson this year!

It's something different to just writing out sums in books.

Students appreciated the chance to work on something challenging:

I liked it because it was hard.

I enjoyed doing a problem that was impossible.

I like the problem because it was very challenging.

Students were motivated to persevere with the problem:

I liked it because you get 36 or 38 so you get determined to get 37.

Yes, as soon as I started I knew I wanted to finish it. I liked thinking about it.

Student saw the potential for learning and understood that working on problems offered the opportunity for gaining new insights:

The maths problem was very frustrating and I enjoyed it. It was fun because you learnt how odd and even numbers work.

When they were asked to suggest helpful hints, it is interesting to notice that many suggestions were in line with the kinds of hints that might be offered by NRICH and were in sympathy with its underlying ethos.

Students recognised the value of the resources that were available to them - their thinking skills and their peers:

Working in silence; having longer thinking time at the beginning.

Talking to more than one person.

Students focused on reducing the routine aspects of the problem and the chances of arithmetical errors. This would enable students to focus on the higher order thinking skills that the problem demands:

A number line.

A calculator.

Students offered comments which drew attention to the underlying mathematical structure of the problem. These are sophisticated hints because they do not give away the solution while encouraging reflection on the way that numbers work:

Think about odd numbers and even numbers.

Think of what happens if you add 2 odd numbers together.

Students offered another problem which offers the same challenge as the original. It acknowledges that insight might come through perseverance with the original and similar problems:

Think and see if you can get up to thirty with seven numbers.

Now we would like to consider the comments made by students who made negative comments about their experience of working on the problem.

Student focused on the arithmetic rather than stepping back and considering the underlying structure of the problem:

I was more trying to add together than looking at the numbers?

Students did not recognise that there was anything to be gained from tackling an "impossible" problem:

I don't really like doing maths problems and it was impossible to do which made it worse.

Being an impossible problem there is no point in doing it because it is pointless sitting there for ages stuck.

Students expressed strong negative feelings about being asked to work on something which did not fit with their preconceptions about what mathematics questions are like:

Was quite annoying when you found out it was impossible.

I love maths and enjoy it very much u gave me that problem to work out and I could't so I was enoyed, but then u tell me its impossible its such a waste of time and effort and Im very enoyed. (sic)

The wording of the question does not suggest that the problem is impossible. The wording could be changed to: "How many ways can you make 37 with ten numbers from the bags?" This would still retain the same level of challenge but does not imply that ten numbers can be found.

When they were asked to suggest helpful hints, it is interesting to notice that many suggestions were not in line with the kinds of hints that might be offered by NRICH and were not in sympathy with its underlying ethos.

Students wanted to remove all the difficulty out of the problem so that there was no challenge left:

A clue to point in the direction of impossibility.

There is no answer.

Don't think it can definitely be done.

U can't do it.

Telling me it was impossible might!!

Student offered a hint that would trivialise the problem and reduce the challenge in a similar way to the hints above. This is an unsophisticated hint as it almost gives away the solution rather than encouraging an exploration of the underlying mathematical structure of the problem:

odd + odd = even

Implications

We started off looking for ways in which a web-based resource like NRICH could offer mediation for non-standard problems. We initially assumed that the mediation that would be necessary would only need to point to the mathematics in the problem and would be in the form of hints. For example:

Spend a few minutes "playing with the problem", trying different numbers.

Have you kept a record of the totals "made"?

What do you notice about your totals?

What can you say about these types of numbers?

Can you make 37 with a different number of numbers? How many?

Can you explain why?

This could serve to mediate between the student and the mathematics by making the mathematics more accessible to the student. But the feedback from some of the students shows that this will not always be enough. This mirrors the analysis of Watson et al (Watson, Geest et al. 2002)who say:

If we imagine learners and mathematics as separated by a gap, and the teacher's job as bringing the two together, then we are talking about the difference between adapting the mathematics so that it can be more easily taken into the world of the learner, and adapting the habits of the learner and classroom so that the learner may be taken more easily into the world of mathematics.

In this project we do more of the latter.

Our results have also highlighted the need to consider doing more of the latter if we are to support students whose preconceptions about mathematics and the nature of working mathematically on new problems do not match the ethos of the NRICH website.

What else can be offered in an online environment which might mirror the strategies used by teachers in classrooms? We have three suggestions:

'? ¢ Metacognitive mediation and advice that spells out some of the assumptions about how students are expected to work. For example:

Don't expect to know what to do immediately,

Try the problem, get your hands dirty... work in rough... talk to someone...

Would making a sketch, a drawing, a table, some notes help?

All the time think, explore... do you notice anything?... any patterns?

Then, step back from the problem...

Really stuck? There are hints available...

Talk to others about what you have done and found out.

This could come before any hints that are specifically related to the problem and would be the first port of call for any students who are stuck. This would serve the purpose of enculturating students into the ethos of the website (De Geest, Watson et al. 2003)

Looking at solutions

This option would direct students to the solution of the problem and invite them to consider it before tackling another problem which shares some significant features with the original problem. An example of a follow up question to "Make 37" could be:

Fibonacci Factors

In the Fibonnaci sequence each term is the sum of the two terms before it:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

Where do the even numbers come in the sequence?

Is there a pattern? Why?

This option offers students a model on which to build their own solution to the new problem. As this example illustrates, the aim would be to offer a problem that is not trivial after seeing the solution to the original. An alternative, that is available on the NRICH website, is to direct students to similar problems that have already been solved and suggest that they use insights from looking at these solutions to help them tackle their current problem.

Participation in webboard discussions

Many students use online resources when working on their own. Talking to others in this context can be difficult but is an option through participation in webboard discussions about problems. This is being trialled on the NRICH website through a special section of the webboard where students are told that:

You can discuss how you are getting on with the problems, and give each other hints, BUT DON'T GIVE AWAY THE ANSWERS!

If you want to check your solution agrees with someone else, you can post it in white "ink". That way, people still working on the problem won't see it, but those who want to can see it by selecting that bit of text.

Conclusion

Jaworski's work (1994) highlights the subtlety and complexity of the teacher's role in the classroom. It is important to recognise that any online mediation will not be able to match the variety of ways in which teachers are able to respond sensitively to their pupils' needs. However, the four suggested mediation strategies do take account of the elements of the teaching triad identified by Jaworski. They seek to manage pupils' learning by offering a range of routes through the problems. In offering students a range of choices, the mediation strategies attempt to be sensitive to their cognitive and emotional needs. They attempt to support the learners while still expecting students to engage with challenging mathematics. In this paper we have signalled the importance of mathematics teaching that attempts to engage and challenge students. We have reported on some students'?? responses to a non-standard problem and suggested that they can be placed along a continuum. We have used our findings to suggest mediation strategies to help students tackle mathematical problems that could be offered on an Internet website like NRICH. These mediation strategies take into account the strategies used by teachers in classrooms. Our future work will assess the effectiveness of these strategies.

References

Ahmed, A. (1987). Better Mathematics. London, HMSO.

Askew, M., M. Brown, et al. (1997). Effective Teachers of Numeracy. London, School of Education, King's College London: 122.

Boaler, J. (1997). Experiencing School Mathematics: Teaching styles, sex and setting. Milton Keynes, Open University Press.

De Geest, E., A. Watson, et al. (2003). Thinking in Ordinary Lessons: What happened when nine teachers believed their failing students could think mathematically. Psychology of Mathematics Education.

Galbraith, P. L. and D. Chant (1990). "Factors Shaping Community Attitudes to Mathematics: Implications for future curriculum change." Educational Studies in Mathematics 21(4): 299-318.

Holt, J. (1964). How Children Fail. London, Penguin.

Jaworski, B. (1994).Investigating Mathematics Teaching: A constructivist enquiry. London, The Falmer Press.

Mason, J., L. Burton, et al. (1985). Thinking Mathematically. Harlow, England, Addison-Wesley.

Silverman, D. (2001). Interpreting Qualitative Data: Methods for Analysing Talk, Text and Interaction. London, Sage.

Strauss, A. and J. Corbin (1990). Basics of Qualitative Research: Grounded Theory procedures and Techniques. Newbury Park, Sage Publications Inc.

Watson, A., E. D. Geest, et al. (2002). Improving attainment in mathematics projet, part 2: developing ways of being mathematical. British Educational Research Association, Exeter, Education-line.