Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Article by Jenni Back, Charlie Gilderdale and Jennifer Piggott
Published 2011
Exploring the Challenge of Online Mediation
This paper will report on students' responses to a mathematical problem from the NRICH website. In particular, we were interested in students' responses to a question that provided an unusual challenge. Their responses have informed our identification of a range of students' attitudes which can be placed along a continuum. We have used the findings to suggest mediation strategies that could be offered on a website to meet the needs of learners throughout the continuum. These mediation strategies take into account the strategies used by teachers in classrooms.
The NRICH Website
NRICH (www.nrich.maths.org.uk) is a web based resource that
aims to provide mathematical enrichment for all people from the age
of 5 onwards. It offers problems that are more interesting and
challenging than those found in standard textbooks in the hope that
students and teachers will appreciate the contribution they can
make to mathematical thinking and understanding. Recent research
has recognized the deficiencies of a mathematics curriculum that is
mainly based on skills and procedures and advocates a curriculum
that offers students more opportunities to be mathematical and that
respects them as responsible learners of mathematics (Ahmed 1987)
(Boaler 1997) (Jaworski 1994) (Askew, Brown et al. 1997) (Watson,
Geest et al. 2002).
Most people's exposure to mathematics is based on their
experiences at school, mainly through textbooks (Galbraith and
Chant 1990). NRICH is offering something different: most of the
mathematics problems on the website cannot be easily pigeon holed
into a chapter in a textbook but require students to use a range of
unspecified skills. Textbooks tend to suggest there is a best way
of doing things and promote a limited number of tried and tested
algorithms. NRICH problems, in contrast, can often be solved by
non-standard methods and in a variety of ways.
What is the impact of this on the people who use NRICH? If
they come with the "school maths" mindset, where they expect to see
a problem and know what to do, they may give up when they do not
know how to proceed. In school the right strategy has generally
been modelled for them in advance whereas the website problems
assume users will take time to think for themselves. In many
classrooms most students know what to do because they are following
a procedure for which they have been trained; there is the
expectation that the majority of students will follow that
procedure successfully. In these classrooms there is often a lot of
mediation at the start of lessons in which teachers prepare
students for what they are about to do and on-going mediation that
offers clarification and reminders.
These features of classroom life are not available to students
tackling problems on the NRICH website. In this online
environment
- users are not told what mathematics to use
- users may be working on their own without support from teacher or peers.
Students who have been brought up in the stereotypical
classroom culture described above will be in an unfamiliar
situation. This paper explores how mediation could be offered on a
website like NRICH without diminishing the challenge to users to
think mathematically.
Thinking mathematically usually requires students to search
for possible methods of attack and to realise the importance of
making conjectures and generalisations. These conjectures may be
tentative and provisional and are open to challenge from others but
they can be developed into results which can eventually be
justified and proved (Mason, Burton et al. 1985) (De Geest, Watson
et al. 2003). There is value in allowing students to pursue their
own individual lines of investigation regardless of the most
efficient way of reaching the solution to a problem. However, we
must acknowledge that this may be a very uncomfortable experience
for them (De Geest, Watson et al. 2003) (Holt 1964).
Mediation
It is necessary to consider the nature of mediation in
teaching and learning contexts. In classrooms, teachers are engaged
in mediating between students and the mathematics: they check that
the students have read the question and that they understand the
task; they suggest a first (or second or third...) move; they
demonstrate connections with previous work or experiences; they
simplify the task or demonstrate an analogous task; they ask
questions to encourage students to pursue fruitful avenues of
enquiry. With different children and different tasks, a very varied
and rich range of possible options is open to teachers.
All this is highly dependent on teachers' professional
judgements about appropriate actions in different contexts. It
involves a sensitive reading of the situation and may be adapted or
altered in subtle ways to match the perceived needs of different
students. Barbara Jaworski (Jaworski 1994) has identified a
teaching triad containing three elements of teachers' professional
practice: management of learning, sensitivity to students and
mathematical challenge. This triad will inform the analysis of the
mediation that can be offered on a website like NRICH.
The Study
To get some sense of what mediation might help, we asked 70
students aged between ten and eleven to try the "Make 37" problem
and then administered a questionnaire that asked them about the
experience of tackling this non-standard problem. The questionnaire
enabled us to collect a large number of responses immediately after
the students had attempted the problem; this ensured that the
experience was easily recollected. We specifically asked them about
what they liked and disliked and for their recommendations for
helpful hints. This generated qualitative data that we analysed
using grounded theory (Silverman 2001) (Strauss and Corbin
1990)
Here is the "Make 37" problem that first appeared on the NRICH
website in 2003 (http://nrich.maths.org/public/viewer.php?obj_id=1885
).
Make 37
Four bags
contain a large number of 1s, 3s, 5s and 7s.
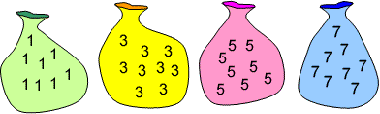
Pick any ten
numbers from the bags above so that their total is 37.
Superficially the problem seems little different from a
standard textbook task asking students to make numbers from smaller
numbers and giving them practice in adding a series of small
numbers together. However it turns out to be rather different from
that and after a little investigation and thought students begin to
realise that the problem might not have a solution after all, and
some eventually decide that it is impossible. As a consequence, the
solution to the problem requires students to provide a convincing
argument that shows why it is impossible.
The Findings: Two Extremes along aContinuum
We have selected quotes from students that can be positioned
on the extremes of a continuum, from very positive to very negative
reactions to the problem.. Initially we would like to consider the
comments made by students who appreciated the experience of working
on the problem.
Students appreciated the chance to work on something
different:
I liked it because the problem made me think harder than I have in a Maths lesson this year!
It's something different to just writing out sums in books.
Students appreciated the chance to work on something
challenging:
I liked it because it was hard.
I enjoyed doing a problem that was impossible.
I like the problem because it was very challenging.
Students were motivated to persevere with the problem:
I liked it because you get 36 or 38 so you get determined to get 37.
Yes, as soon as I started I knew I wanted to finish it. I liked thinking about it.
Student saw the potential for learning and understood that
working on problems offered the opportunity for gaining new
insights:
The maths problem was very frustrating and I enjoyed it. It was fun because you learnt how odd and even numbers work.
When they were asked to suggest helpful hints, it is
interesting to notice that many suggestions were in line with the
kinds of hints that might be offered by NRICH and were in sympathy
with its underlying ethos.
Students recognised the value of the resources that were
available to them - their thinking skills and their peers:
Working in silence; having longer thinking time at the beginning.
Talking to more than one person.
Students focused on reducing the routine aspects of the
problem and the chances of arithmetical errors. This would enable
students to focus on the higher order thinking skills that the
problem demands:
A number line.
A calculator.
Students offered comments which drew attention to the
underlying mathematical structure of the problem. These are
sophisticated hints because they do not give away the solution
while encouraging reflection on the way that numbers work:
Think about odd numbers and even numbers.
Think of what happens if you add 2 odd numbers together.
Students offered another problem which offers the same
challenge as the original. It acknowledges that insight might come
through perseverance with the original and similar problems:
Think and see if you can get up to thirty with seven numbers.
Now we would like to consider the comments made by students
who made negative comments about their experience of working on the
problem.
Student focused on the arithmetic rather than stepping back
and considering the underlying structure of the problem:
I was more trying to add together than looking at the numbers?
Students did not recognise that there was anything to be
gained from tackling an "impossible" problem:
I don't really like doing maths problems and it was impossible to do which made it worse.
Being an impossible problem there is no point in doing it because it is pointless sitting there for ages stuck.
Students expressed strong negative feelings about being asked
to work on something which did not fit with their preconceptions
about what mathematics questions are like:
Was quite annoying when you found out it was impossible.
I love maths and enjoy it very much u gave me that problem to work out and I could't so I was enoyed, but then u tell me its impossible its such a waste of time and effort and Im very enoyed. (sic)
The wording of the question does not suggest that the problem
is impossible. The wording could be changed to: "How many ways can
you make 37 with ten numbers from the bags?" This would still
retain the same level of challenge but does not imply that ten
numbers can be found.
When they were asked to suggest helpful hints, it is
interesting to notice that many suggestions were not in line with
the kinds of hints that might be offered by NRICH and were not in
sympathy with its underlying ethos.
Students wanted to remove all the difficulty out of the
problem so that there was no challenge left:
A clue to point in the direction of impossibility.
There is no answer.
Don't think it can definitely be done.
U can't do it.
Telling me it was impossible might!!
Student offered a hint that would trivialise the problem and
reduce the challenge in a similar way to the hints above. This is
an unsophisticated hint as it almost gives away the solution rather
than encouraging an exploration of the underlying mathematical
structure of the problem:
odd + odd = even
Implications
We started off looking for ways in which a web-based resource
like NRICH could offer mediation for non-standard problems. We
initially assumed that the mediation that would be necessary would
only need to point to the mathematics in the problem and would be
in the form of hints. For example:
Spend a few minutes "playing with the problem", trying different numbers.
Have you kept a record of the totals "made"?
What do you notice about your totals?
What can you say about these types of numbers?
Can you make 37 with a different number of numbers? How many?
Can you explain why?
This could serve to mediate between the student and the
mathematics by making the mathematics more accessible to the
student. But the feedback from some of the students shows that this
will not always be enough. This mirrors the analysis of Watson et
al (Watson, Geest et al. 2002)who say:
If we imagine learners and mathematics as separated by a gap, and the teacher's job as bringing the two together, then we are talking about the difference between adapting the mathematics so that it can be more easily taken into the world of the learner, and adapting the habits of the learner and classroom so that the learner may be taken more easily into the world of mathematics.
In this project we do more of the latter.
Our results have also highlighted the need to consider doing
more of the latter if we are to support students whose
preconceptions about mathematics and the nature of working
mathematically on new problems do not match the ethos of the NRICH
website.
What else can be offered in an online environment which might
mirror the strategies used by teachers in classrooms? We have three
suggestions:
- '? ¢ Metacognitive mediation and advice that spells out some of the assumptions about how students are expected to work. For example:
Don't expect to know what to do immediately,
Try the problem, get your hands dirty... work in rough... talk to someone...
Would making a sketch, a drawing, a table, some notes help?
All the time think, explore... do you notice anything?... any patterns?
Then, step back from the problem...
Really stuck? There are hints available...
Talk to others about what you have done and found out.
This could come before any hints
that are specifically related to the problem and would be the first
port of call for any students who are stuck. This would serve the
purpose of enculturating students into the ethos of the website (De
Geest, Watson et al. 2003)
- Looking at solutions
This option would direct students
to the solution of the problem and invite them to consider it
before tackling another problem which shares some significant
features with the original problem. An example of a follow up
question to "Make 37" could be:
Fibonacci Factors
In the Fibonnaci sequence each term is the sum of the two terms before it:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
Where do the even numbers come in the sequence?
Is there a pattern? Why?
This option offers students a model
on which to build their own solution to the new problem. As this
example illustrates, the aim would be to offer a problem that is
not trivial after seeing the solution to the original. An
alternative, that is available on the NRICH website, is to direct
students to similar problems that have already been solved and
suggest that they use insights from looking at these solutions to
help them tackle their current problem.
- Participation in webboard discussions
Many students use online resources
when working on their own. Talking to others in this context can be
difficult but is an option through participation in webboard
discussions about problems. This is being trialled on the NRICH
website through a special section of the webboard where students
are told that:
You can discuss how you are getting on with the problems, and give each other hints, BUT DON'T GIVE AWAY THE ANSWERS!
If you want to check your solution agrees with someone else, you can post it in white "ink". That way, people still working on the problem won't see it, but those who want to can see it by selecting that bit of text.
Conclusion
Jaworski's work (1994) highlights the subtlety and complexity
of the teacher's role in the classroom. It is important to
recognise that any online mediation will not be able to match the
variety of ways in which teachers are able to respond sensitively
to their pupils' needs. However, the four suggested mediation
strategies do take account of the elements of the teaching triad
identified by Jaworski. They seek to manage pupils' learning by offering a
range of routes through the problems. In offering students a range
of choices, the mediation strategies attempt to be sensitive to their cognitive and emotional
needs. They attempt to support the learners while still
expecting students to engage with challenging mathematics. In this paper
we have signalled the importance of mathematics teaching that
attempts to engage and challenge students. We have reported on some
students'?? responses to a non-standard problem and suggested that
they can be placed along a continuum. We have used our findings to
suggest mediation strategies to help students tackle mathematical
problems that could be offered on an Internet website like NRICH.
These mediation strategies take into account the strategies used by
teachers in classrooms. Our future work will assess the
effectiveness of these strategies.
References
Ahmed, A. (1987). Better
Mathematics. London, HMSO.
Askew, M., M. Brown, et al. (1997). Effective Teachers of Numeracy.
London, School of Education, King's College London: 122.
Boaler, J. (1997). Experiencing School Mathematics: Teaching
styles, sex and setting. Milton Keynes, Open University
Press.
De Geest, E., A. Watson, et al. (2003). Thinking in Ordinary Lessons: What happened
when nine teachers believed their failing students could think
mathematically. Psychology of Mathematics Education.
Galbraith, P. L. and D. Chant (1990). "Factors Shaping
Community Attitudes to Mathematics: Implications for future
curriculum change." Educational
Studies in Mathematics 21(4): 299-318.
Holt, J. (1964). How
Children Fail. London, Penguin.
Jaworski, B. (1994).Investigating Mathematics Teaching: A
constructivist enquiry. London, The Falmer Press.
Mason, J., L. Burton, et al. (1985). Thinking Mathematically. Harlow,
England, Addison-Wesley.
Silverman, D. (2001). Interpreting Qualitative Data: Methods for
Analysing Talk, Text and Interaction. London, Sage.
Strauss, A. and J. Corbin (1990). Basics of Qualitative Research: Grounded
Theory procedures and Techniques. Newbury Park, Sage
Publications Inc.
Watson, A., E. D. Geest, et al. (2002). Improving attainment in mathematics projet,
part 2: developing ways of being mathematical. British
Educational Research Association, Exeter, Education-line.