Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Caterpillars
Age 5 to 7
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Caterpillars

Well, here are the caterpillars!
Our caterpillars have numbers on each little part - numbers $1, 2, 3, 4, \ldots$ up to $16$.
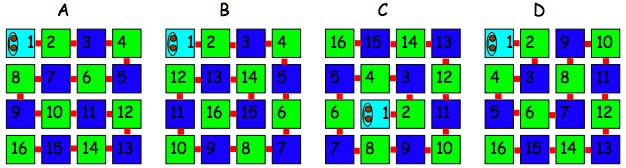
You can see their pale blue head, and their body bending at right angles so that each part is lying in a square.
There are two explorations to go with these caterpillars:
1. You could look carefully at the shapes of the caterpillars and let them turn in other ways. Here are a few to start you off:

When you've discovered many new ones, with the shapes - and therefore the numbers - all showing differently, you could compare them. What is the same and what is different? Can you explain why?
You could try to put the caterpillars in shapes that are not squares!
OR
2.
a) Choose one of the caterpillars and, using the numbers and the way that they are arranged, explore the patterns and relationships you can find.
b) Then let that caterpillar grow nine more parts so that it becomes a $25$ caterpillar with the shape bending in just the same way. Explore those patterns and relations.
c) Finally, compare the two different groups of things you've discovered in a) and in b).
Do tell us about all the things you find out.
Why do this problem?
This investigation is likely to capture the attention of many children and you might discover that they find things to explore which had not occurred to you! It is also an enriching activity that has links both with spatial awareness, number awareness and number patterns. It could be used to broaden pupils'
experiences of number relationships.
Possible approach
You could introduce this investigation by drawing a caterpillar on a grid, perhaps on the interactive whiteboard, to establish the context. Invite a child to draw a different caterpillar on another grid and then ask pairs to talk about what they notice.
This leads into the first activity so this could be pursued further by the group, or some might prefer to opt for the second activity. You will need to have some conversations about how they might record what they have found. Having squared paper available, or perhaps some templates of different sized grids, would be a good idea, but children might have their own suggestions.
Key questions
What do you see?
Tell me about the numbers you've.
I like this shape of caterpiller you've made, tell me about it.
Possible extension
Alan Parr (who has contributed many fantastic ideas to NRICH), also sent the following suggestions for investigating the Caterpillars in other ways:
- If a caterpillar has some segments which are black then you won't be able to see their numbers, so you can offer problems with missing numbers. You can have a surprisingly large number of missing numbers and still be able to fill in every one. For example, in caterpillar A you only need to know the $1, 5, 10,$ and $11$ and you can place all the other numbers. You could challenge children to fill in the rest of the numbers, but also invite them to make their own so that they give as few numbers as possible in order for a friend to be able to complete the caterpillar. You could also extend this to larger caterpillars!
- For a tougher challenge, you could change the caterpillars so that you can't see the individual segments, only four mega-sections each of which covers four segments in a $2 \times 2$ square. Each mega-section shows you the product of the four segments of the caterpillar. For example, the top-left quarter shows $24$, top-right $7920$, bottom-right $15288$, bottom-left $7200$. Can learners identify the number of each segment? (Alan attributes this idea to Mike Taylor - thank you!) You could also set this up in a "battleships-style" game where each player records a caterpillar in a square grid and player $1$ tells player $2$ the products of $2\times2$ blocks he/she asks about, and vice versa.
Possible support
Here are some ideas to use if the pupils are new to the exploration of number patterns:

These show:
Adding horizontally, then vertically;
Adding in slanting lines - when you've done the two different sets, [North West to South East and then North East to South West] you can put them together in different ways;
Adding in squares and putting down the answer in a square. So, adding in a $2$ by $2$ square and performing all $9$ additions we would have:

There are lots of questions to be asked here, based on trying to explain the resulting totals.
Adding in $3$ by $3$ squares as above.