 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Rectangular Pyramids



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
A proof of this result came from students from the Key Stage 3 Maths Club at Strabane Grammar School, Northern Ireland and the following one from Joel, ACS (Barker) Singapore:
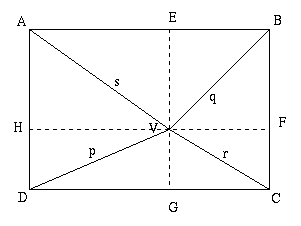
(a) In the diagram given (in 2 dimensions) p 2 + q 2 = r 2 + s 2
Proof
Draw 2 lines through V parallel to the edges of the rectangle, dividing the figure into four pairs of right-angled triangles. Label the point on AB as E, on BC as F, on CD as G and on DA as H. By Pythagoras theorem:
| p 2 = DG 2 +DH 2 |
| q 2 = BE 2 + BF 2 |
| r 2 = CF 2 + CG 2 |
| s 2 = AE 2 + AH 2 |
Since DG=AE, CG=BE, AH=BF and CF=DH,
p 2 + q 2 = AE 2 + CF 2 + CG 2 + AH 2 = r 2 + s 2
(b) If the diagram represents a pyramid on a rectangular base where p, q, r and s are the lengths of the sloping edges then the result p 2 + q 2 = r 2 + s 2 still holds true.
Proof
Let V 1 be the foot of the perpendicular from V to the base ABCD of the pyramid and let h be the height of the pyramid so that VV 1 = h and let V 1 A = s 1 , V 1 B = q 1 , V 1 C = r 1 , and V 1 D= p 1 .
By Pythagoras theorem we have: p 1 2 + h 2 = p 2 , q 1 2 + h 2 = q 2 , r 1 2 + h 2 = r 2 and s 1 2 + h 2 = s 2 .
Using the result already proved in 2dimensions, that is
p 1 2 + q 1 2 = r 1 2 + s 1 2 ,
we get p 1 2 + q 1 2 + 2h 2 = r 1 2 + s 1 2 + 2h 2
so p 2 + q 2 = r 2 + s 2 .
You may also like
Some(?) of the Parts
A circle touches the lines OA, OB and AB where OA and OB are perpendicular. Show that the diameter of the circle is equal to the perimeter of the triangle
Baby Circle
A small circle fits between two touching circles so that all three circles touch each other and have a common tangent? What is the exact radius of the smallest circle?
Logosquares
Ten squares form regular rings either with adjacent or opposite vertices touching. Calculate the inner and outer radii of the rings that surround the squares.