Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Article by Jennifer Piggott
Published 2011
Mathematics Enrichment: What Is it and Who Is it For?
Mathematics enrichment: what is it and who is it for?
Jennifer Piggott, University of
Cambridge, Faculty of Education (jsp38@cam.ac.uk)
NRICH Mathematics Project
(www.nrich.maths.org)
1. Abstract
The NRICH Project (www.nrich.maths.org) has been in operation since 1996. Its original purpose was to support able young mathematicians whose access to mathematics related opportunities in their local community was limited. The intention was to offer an online community where they could talk about and do mathematics with like-minded youngsters and this remains a principle aim of the project today. Since 1996 the resources on the web site have grown and the project has developed a reputation for creative thinking in the area of mathematics enrichment both nationally and internationally.
Over the last two years we have been carrying out a review of the project with the purpose of identifying ways of using and developing existing resources and creating new ones that are in keeping with our views on enrichment. This paper reflects the findings of this study, which is still underway and which has been running in parallel with the review and development cycle. I have used data from discussions and interviews and artefacts (problems and resources) alongside a literature review support the view of enrichment curriculum offered in this article. The research and development process has resulted in a questioning of our initial understandings of mathematics enrichment as well as views expressed within the current literature. The study identified the need to give coherence to terms such as "problem solving" and "mathematical thinking" as concepts which were felt to underpin "enrichment". I present here an overview of these aspects of the study, alongside our views of teaching for enrichment and learning through enrichment and whether these relate solely to the most able.
2. Introduction
The literature on enrichment, problem solving and mathematical
thinking lacks clarity because it fails to give consistent
interpretations of each of the terms. Often the terms are used in a
way which assumes the reader's interpretation of the phrases
"problem solving" or "mathematical thinking" are the same as the
author's, although Schoenfeld (1992) is a rare case where a
distinction is made, although not a distinction shared by this
paper. The word "enrichment" is almost exclusively used in the
context of provision for the mathematically most able, with a few
notable exceptions such as Wallace (1986). The implication taken
from this general lack of clarity, is that the concepts are tightly
bound and therefore difficult to separate. My aim is to place them
into a meaningful framework to inform future discussion. There are
three questions which I will take from this:
- What, if any, is the difference between the terms "enrichment", "mathematical thinking" and "mathematical problem solving"
- If there is distinction between these terms, can we place them in some meaningful relationship with each other?
- Are the processes they represent simply the domain of the mathematically most able?
3. Defining a Framework
The experience of most students "doing mathematics" involves
studying materials and working through tasks set by others (Olkin
and Schoenfeld 1994) with very little room for the entrepreneur or
creative thinker.
One of the things we at NRICH are trying to offer in an
enrichment curriculum is the opportunity to experience:
"The joy of confronting a novel
situation and trying to make sense of it - the joy of banging your
head against a mathematical wall, and then discovering that there
may be ways of either going around or over that wall"
Page 43
Schoenfeld (1994)
However, to achieve this, we need to know what will make this
happen. It is therefore necessary to make explicit the content and
nature of the skills, knowledge and classroom experience and
identify the methodologies for implementation. What do the
curriculum resources and learning tools look like that help
students come to "know"? in this way?
Enrichment is associated by some with models of curriculum
acceleration or compaction. However, I do not describe either of
these curriculum approaches as enrichment. Acceleration means that
students are given access to "standard curriculum material" earlier
and are encouraged to move more quickly through subject content,
normally resulting in early entry to nationally recognised
examinations. Curriculum compaction (Renzulli and Reis 1999) more
usually restructures a curriculum in a way that enables students to
cover aspects of the standard curriculum "more efficiently". This
is often accomplished by clustering related curriculum themes
vertically. In the cases of acceleration and compaction, the result
is the release of time which can then be used for extra curricular
activities. It is not the acceleration or the compaction that
concerns enrichment but what happens in the time created by such
approaches and "doing more of the same" is not enrichment.
Sometimes the time created is used for activities involving problem
solving and/or curriculum extension (where students work on
mathematics that they will generally not meet in the standard
curriculum). However, here the model of enrichment is still viewed
as an add on. This denies the vast majority of students access to
enrichment opportunities and imposes significant organisational
pressures within the classroom. There is also little evidence
available to suggest that schemes of acceleration result in any
long term benefit to the students involved. If problem solving and
mathematical thinking linked to stimulating mathematical contexts
is worth doing, surely it is worth doing for everyone a significant
proportion of the time. Enrichment should pervade the curriculum as
a whole and not simply be available to those who work fastest. If
this is to be the case we need not only to consider enrichment as a
vehicle for the most able but, for the sake of classroom
management, if it can offer something to the vast majority of
students it will, at the very least make it a more realistic
option. This does have very significant issues for the type and
scope of resources that are used to support enrichment activities
and the development of materials forms part of the research upon
which this paper is based. Here though I will focus first on what
we mean by problem solving and mathematical thinking.
3.1 Problem Solving and Mathematical Thinking?
The aim of this section of the paper is to offer a definition of enrichment. I will first spend some time reviewing what I am taking as the constituent concepts of an enrichment curriculum including problems, problem solving. Then I will briefly consider some implications for teaching and learning and finally I will present a framework for enrichment.3.1.1 The problem and the problem solver
The view of problems offered by some authors as "authentic" or
"real world" (Blum and Niss 1991), or "word" problems (Riley,
Greeno et al. 1983; Doyle 1988; Mayer 2002) is not seen as core to
the nature of a problem, but simply contexts in which problems are
offered. That is not to forget that it is crucial for problems to
engage and "inspire" the student to think the struggle of problem
solving is worthwhile. Neither is this simply about the problems in
isolation but also about pupils and teaching approaches that
encourage a non-mechanical or simplistic view of mathematics.
Many authors (Polya 1957; Riley, Greeno et al. 1983; Mayer
2002) describe a problem as a problem because it has a goal (the
solution) and the student does not have the "right" sort of
knowledge to be able to solve it immediately. The "right" knowledge
is both the mathematical concept knowledge and the problem solving
knowledge. Schoenfeld, and Blum and Niss, Schoenfeld (1985; 1991;
1992) refer to problems as being "relative" to the individuals
knowledge and experience.
"A problem is not inherent in a task but depends on the
individual."
Page 74
Schoenfeld (Schoenfeld 1985)
Referring to the report of the Problem Solving Theme Group at
the ICME 5, Mason and Davis (1991) stress the importance of the
autonomy of the solver in terms of what they try to do and what
constitutes for them a satisfactory end point. This centring on the
solver is reflected in the paper by Pape, Bell et al (2003) who
suggest that pupils should see themselves as agents in their own
learning when problem solving.
It is this idea of a problem as something that needs to be
worked on without a clear idea on the part of the solver, at least
to start with, about how to find the solution that is key. However,
for a problem to be effective it also needs to engage, be
accessible (enable the pupil to step into the problem) and be
accompanied by the necessary support to help progress towards a
solution with the pupil leading rather than being led. No matter
how good on a superficial level a problem might be (relevant,
timely, well structured, clear) if the student cannot engage with
it because it starts at a point beyond their zone of proximal
development (Vygotsky 1978) then no amount of support will result
in a learning gain. If, in addition it does not offer scope for the
varying learning needs and levels of knowledge of a group of
students then it is unlikely to be of value in a classroom setting.
In this case some students will not be able to engage at all some
will eventually solve the problem, and the most able will have
finished five minutes after the start of the lesson, because to
them the problem was not even a problem.
3.1.2 Problem solving
"more important than specific mathematical results are the
habits of mind used by people who create those results"
Cuoco,
Goldenberg et al. Page 375 (1996)
There have been a number of attempts to describe the problem
solving process, possibly starting in 1933 by Dewey with his five
stage model. These five stages have much in common with the work of
Polya (1957), who expounded and related a four element model. Those
four elements were; understanding the problem, devising a plan,
carrying out the plan and looking back. Polya also went on to look
at particular techniques that can prove useful within each of these
elements. More recently Mayer (2002), who offers a similar model to
Polya's in his "componential theory of problem solving", considers
similar "elements". Much of the problem solving literature either
develops of reiterates these basic "elements" and guidance in
tackling mathematical problems.
In essence I am advocating problem solving as an iterative
process based on identifiable elements, similar to those of Polya
and others including Wilson, Fernandez et al. (C1991 ??), Mason et
al (1985), Mayer (2002), Ernest (2000). That is not to suggest that
many of these models were intended to be purely linear, as Wilson
et al. (ibid.) suggest with reference to Polya's four element
model. Hence the deliberate choice of the term "element" rather
than "stage" in this text. These references have many common
threads and have models of the process broken down into a varied
number of elements. The elements outlined below combine a number of
the features of these existing models with our own research
findings. This, it must be emphasised, is meant to convey a sense
of direction but is not linear. The intention is that the solver
may need to revisit elements and reformat the problem as they work
towards a solution - giving an iterative feel to the problem
solving process.
The C.A.P.E.
model
Comprehension
- Making sense of the problem/retelling/creating a mental image,
- Applying a model to the problem;
Analysis and synthesis
- Identifying and accessing required pre-requisite knowledge,
- Applying facts and skills, including those listed in mathematical thinking (above),
- Conjecturing and hypothesising (what if);
Planning and execution
- Considering novel approaches and/or solutions
- Identifying possible mathematical knowledge and skills gaps that may need addressing,
- Planning the solution/mental or diagrammatic model,
- Execute;
Evaluation
- Reflection and review of the solution,
- Self assessment about ones own learning and mathematical tools employed,
- Communicating results.
3.1.3 The roles of Problem solving
The place of problem solving is a key one not only in terms of
the skills it is possible to develop but also in its role as
supporting learning in other areas. These types of generic teaching
and learning contexts for problem solving include considering it as
a skill to be learned or as a tool to learn through. Authors who
consider these roles for problem solving in more depth include:
Stanic and Kilpatrick (1988), Nunokawa (2004); Wilson, Fernandez et
al. (1991) Blum and Niss (1991) . From this literature it is
possible to identify the following roles:
- Problem solving as a means of learning mathematical content -teaching through problem solving.
- Problem solving in order to learn about the processes of problem solving (the formative argument of Blum and Niss) -teaching about.
- Problem solving as a generic skill applicable to other subjects as well as mathematics and offering the ability to take a critical view of the world (utility argument) - teaching for.
- Problem solving as a motivational tool -to give relevance to other aspects of mathematics.
- Problem solving as a fundamental part of mathematics.
Although this list merits a much more detailed discussion its
inclusion here is simply to highlight the range of reasons we might
engage in problem solving. I am not assuming that "problem solving"
is simply seen as being about solving problems but it can also be
about learning to solve problems.
3.2 Mathematical thinking
There is a lack of distinction in the literature between
problem solving and mathematical thinking, with the two terms often
used synonymously. An exception to this however is Schoenfeld
(1992; 1994), who suggests that mathematical thinking
involves:
developing a mathematical point of view - valuing the process
of mathematization (defined in Romberg (1994) from Freudenthal) and
abstraction and having the predilection to apply them,
developing competence with tools of the trade and using those
tools in the service of the goal or understanding structure-
mathematical sense making.
In Schoenfeld's terms problem solving is part of mathematical
thinking. This gives mathematical thinking an overarching role in
which problem solving skills are necessary and could be described
as "the tools of the trade". One concern I have with this model is
that it is not articulating the complexity of what he is describing
as problem solving. I will refer to these two points as
"mathematical literacy" and reserve "mathematical thinking" to
describe the heuristics which underpin mathematical problem
solving. That is, to use mathematical thinking as a term which
covers the specific mathematical skills we engage with when we
problem solve. In this framework mathematical thinking would
encompass some of the ideas suggested by Mason and Davis (1991),
Ramsey (2004) and Polya (1957) Carpenter, Ansell et al. (1993)
including:
- Specialising (specific action that comes out of the problem - doping a particular thing to help to simplify or trying special cases -e.g. paper folding)
- Generalising (as identifying patterns - general or common patterns -formula -looking for an essential shape or form)
- Using analogy (looking at other problems that may have similar structures or develop similar ideas)
- Visualising (using pictures to represent or explain mathematical problem situations or their solutions)
- Identifying the particular
- Modelling
- Decomposing
There is still some work to do in identifying different
aspects of mathematical thinking. Not all the strategies we have
identified have a similar feel to them. Currently it seems easier
to implement a developmental schema for some than for others. We
are will underway in writing materials that support the development
of skills such as "generalising" and "being systematic" but other
skills, such as modelling and decomposing, are proving more
difficult. It may therefore be necessary to subdivide mathematical
thinking into more specific and more general (less well defined)
skills. These and many other elements within our mathematical
thinking list require more research.
3.3 Implications for teaching for enrichment
I have discussed above the curriculum content associated with
mathematical enrichment in terms of the two aspects of mathematical
thinking and problem solving. For this content to have meaning, the
learning (and teaching) environment needs to encourage effective
use of the resources so that pupils develop the necessary skills,
strategies and competence to tackle problems and use underpinning
thinking skills effectively. This has implications for the second
thread of mathematical enrichment -that of the teaching approach
adopted.
This approach reflects constructivist views of learning
through social interaction. This construction of knowledge implies
that learning builds upon the previous knowledge of the student and
their interaction with resources and interaction with members of
their community of practice.
The importance of social interaction during successful problem
solving is not normally associated with constructivist views of
learning, although von Glaserfeld (1995) would deny the correctness
of this claim. In itself, the structure of a "good" problem, where
students are required to interact and build solution schemas,
revisiting and revising ideas, links closely with building on prior
knowledge and the constructing of mental patterns associated with a
rationalist view of knowledge.
What emerges from the literature, is that students'
expectations of mathematics focus on activities that value
procedures and accuracy, that are led by the teacher and that do
not involve social activity. As they value relatively highly the
views of their peers (Adhami, Johnson et al. 1995) social
interaction dominated by the teacher is likely to result in limited
learning gains compared to carefully constructed learning
opportunities where pupils feel autonomous and independent and
teachers act as guides. The problem here is how to move away from
the norm of teacher-centred classroom practice. To be successful,
problem solvers need to be creative, confident and autonomous
(Mason and Davis 1991; Pape, Bell et al. 2003).
"In sum, novel work stretches the limits of classroom
management and intensifies the complexity of the teacher's task of
orchestrating classroom events"
Page 174 (Doyle
1988).
What I am suggesting is that the teacher has a key role to
play in offering the right material at the right time in the right
classroom environment. The classroom environment should facilitate
constructivist approaches through social interaction of the pupils
and teachers. The teacher's role is to offer suitable tasks, create
an atmosphere where students are not passive and use interventions
that do not lead but draw mathematics from the students by making
mathematical connections and help them to fill knowledge
gaps.
This places an emphasis on teaching which stresses:
- non-assertive mediation,
- group work, discussion, communicating...,
- varied solutions and different approaches being valued and utilised,
- exploration, making mathematical connections, extending boundaries, celebrating ideas not simply answers, flexibility...,
- acknowledgment that maths is hard but success is all the more enjoyable when a hurdle is overcome.
3.4 Enrichment
In terms of content I am therefore proposing a framework for
enrichment which comprises two factors, content and teaching. In
terms of content problem solving covers the generic range of
skills, which have applicability within and beyond the mathematics
curriculum and which describe the key elements in the process of
problem solving. Mathematical thinking relates to specific
mathematical skills students need to draw on in order to problem
solve effectively (See Figure 1). Hence, if you were teaching about
problem solving, it would not be enough to learn the generic
problem solving skills but you would also need the mathematical
thinking toolbox, without which problem solvers have no skills to
apply to the problem solving process.
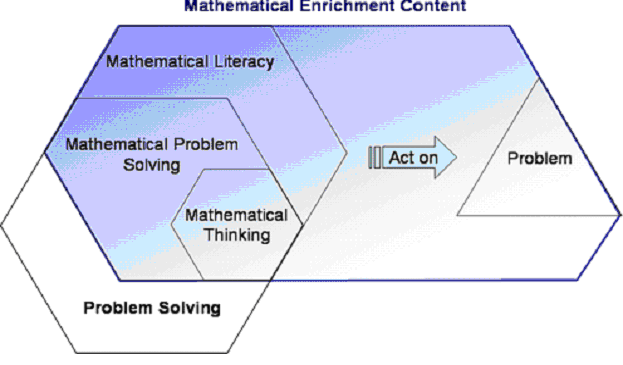
Figure 1
The elements in the figure are then acted on and act on the teacher and the problem solver.
An enrichment curriculum therefore has three content threads
and a particular view of teaching and learning that supports
problem solving:
Content:
- Engaging problems which:
- develop and use problem solving strategies,
- encourage mathematical thinking.
A teaching approach which encourages:
- an open and flexible environment where we encourage:
- group work,
- exploration,
- mathematical communication,
- the valuing and utilisation of difference as a teaching tool,
- the acknowledgment that mathematics is often hard.
Enrichment is not simply learning facts and demonstrating
skills. Mathematical skills and knowledge can be a precursors to,
and also outcomes of, an enrichment curriculum (needs driven
learning). See Figure 2.
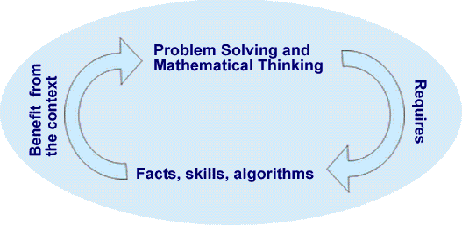
Figure 2
The aim of an enrichment curriculum is to support:
- a problem solving approach (either through, about or for problem solving) that encompasses the four element model,
- improving pupil attitudes
- a growing appreciation of mathematics as a discipline
- the development of conceptual structures that support mathematical understanding and thinking
Enrichment therefore represents an open and flexible approach
to teaching mathematics which encourages experimentation and
communication
4. Implications for Implementation - is for the most able?
There is nothing above that either implies enrichment should
be an add-on or reserved for the special lesson, nor does there
appear to be any reason to believe its exclusivity to pupils of
higher ability. There is also a growing body of evidence that
problem solving approaches and mathematical thinking offered can
benefit all pupils (e.g. Schoenfeld 1994; Renzulli and Reis 1999;
Landau, Weissler et al. 2001) including low-attaining ones (Watson
2001; Watson 2001). This is also supported by our own work with
teachers and pupils when using materials from the NRICH site
(www.nrich.maths.org). therefore, if problem solving is seen as a
fundamental constituent of enrichment then at the very least this
aspect of enrichment can be shown to benefit everyone.
5. Conclusion
In this paper I have therefore attempted to make a case for
saying that enrichment should pervade all aspects of our teaching
and pupils' learning, whatever the ability of the pupil. It
reflects a view of mathematics as a problem solving subject. It can
facilitate developing high level mathematical problem solving and
thinking skills in the most able whilst offering opportunities for
everyone to engage at an appropriate level. This does place high
demands on teachers but in many ways such an approach, given
appropriate resources, may ease the burdens of multiple and
different activities going on in any classroom because of the
different needs of different learners. To implement such a view in
a practicable way, we need to develop appropriate resources. This
is part of the work currently being undertaken by the NRICH
project. We have produced enrichment "trails" that aim to support
pupils with developing thinking skills such as "being systematic",
"generalising", "visualising" and "using analogy" as well as trails
based on learning through problem solving, such as "finding areas
of triangles".
Bibliography
Adhami, M., D. C. Johnson, et al. (1995). Cognitive
Intervention in School Mathematics: Towards a Theory of Teaching.
CAME Project, Mathematics
Education, King's College London : 22.
Blum, W. and M. Niss (1991). "Applied Mathematical Problem
Solving, Modelling, Applications, and Links to Other Subjects -
State, Trends and Issues in Mathematics Instruction." Educational Studies in Mathematics
22: 37-68.
Carpenter, T., P, E. Ansell, et al. (1993). "Models of Problem
Solving: A Study of Kindergarten Children's Problem-Solving
Processes." Journal of Research
in Mathematics Education 24( 5): 428-441.
Cuoco, A., E. P. Goldenberg, et al. (1996). "Habits of Mind:
An Organizing Principle for Mathematics Curricula." Journal of Mathematical Behaviour
15: 375-402.
Doyle, W. (1988). "Work in Mathematics Classes: The Context of
Students' Thinking During Instruction." Educational Psychologist 23( 2): 167-180.
Landau, E., K. Weissler, et al. (2001). "Impact of an
enrichment program on intelligence, by sex, among low SES
population in Israel." Gifted
Education International 15( 2): 207-213.
Mason, J. and J. Davis (1991). Fostering and Sustaining Mathematical
Thinking Through Problem Solving , Deakin University
Press.
Mayer, R. E. (2002). Mathematical Problem Solving.
Mathematical cognition .
J. M. Royer. Greenwich, CT, Information Age Publishing.:
69-92.
Nunokawa, K. (2004). Mathematical Problem Solving and
Learning . ICME 10 - Topic Study Group 18, Copenhagen.
Olkin, I. and A. Schoenfeld, H. (1994). A Discussion of Bruce
Reznick's Chapter [Some Thoughts on Writing for the Putnam].
Mathematical Thinking and Problem
Solving . A. Schoenfeld, H. Hillside NJ, Lawrence Erlbaum:
39-51.
Pape, S., C. Bell, et al. (2003). "Developing Mathematical
Thinking and Self-regulated Learning: A teaching experiment in a
seventh grade mathematics classroom." Educational Studies in Mathematics
53 : 179-202.
Polya, G. (1957). How to
Solve it , Princeton University Press.
Ramsey, Y. (2004). Promoting
Excellence in Mathematical Thinking \in the School System in
Trinidad and Tobago . Critical Thinking, University of the
West Indies.
Renzulli, J., S and S. Reis, M (1999). The Schoolwide
Enrichment Model - Executive Summary. 2004.
Riley, M., S, J. Greeno, G., et al. (1983). Development of
Children's Problem Solving Ability in Arithmetic. The Development of Mathematical
Thinking . H. Ginsberg, Academic Press Inc: 153-196.
Romberg, T., A, (1994). Classroom instruction that fosters
mathematical thinking and problem solving: Connections between
theory and practice. Mathematical
thinking and problem solving . A. Schoenfeld, H. Hillsdale,
NJ, Lawrence Erlbaum Associates.: 287-304.
Schoenfeld, A., H. (1985). Mathematical Problem Solving . Orlando
l, Academic Press.
Schoenfeld, A., H. (1994). Reflections on doing and teaching
mathematics. Mathematical
Thinking and Problem Solving . A. Schoenfeld, H. Hillsdale,
NJ, Lawrence Erlbaum Associates.: 53-69).
Schoenfeld, A. H. (1992). Learning to think mathematically:
Problem solving, metacognition and sense-making in mathematics.
Handbook of reserach on
mathematics teaching and learning . D. A. Grouws. New York,
Macmillan: 334-370.
Stanic, G. and J. Kilpatrick (1988). Historical perspectives
on problem solving in the mathematics curriculum. Teaching and learning mathematical problem
solving: Multiple research perspectives . R. Charles and E.
Silver. Reston VA, National Council of Teachers of Mathematics:
1-22.
von Glasersfeld, E. (1995). Radical Constructivism: A Way of Knowing and
Learning . London, RoutledgeFalmer.
Vygotsky, L. S. (1978). Mind
in Society . Cambridge Mass, Harvard University Press.
Wallace, B. (1986). "curriculum enrichment then curriculum
extension: differentiated educational development in the context of
equal opportunities for all children." Gifted Education International
4: 4-9.
Watson, A. (2001). "Low Attainers exhibiting higher-order
mathematical thinking." Support
for Learning 16
(4): 183.
Watson, A. (2001). "Supporting mathematical thinking
(editorial)." Support for
Learning 16( 1):
2-3.
Wilson, J., W, M. Fernandez, L, et al. (1991). Mathematical
Problem Solving, Department of Mathematics Education, The
University of Georgia. 2004.
Wilson, J., W, M. Fernandez, L, et al. (C1991 ??).
Mathematical Problem Solving, Department of Mathematics Education,
The University of Georgia. 2004.