 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Published 2011 Revised 2023
I'm Stuck!
When looking back on their mathematical experiences, we would be pleased if our pupils were able to say that they had an introduction to the subject which prepared them well for the future at whatever level was appropriate to their needs. There is no doubt that this involves more than being able to answer standard test questions. It includes pupils feeling empowered to work independently, try
things out, and not think there is something wrong when they get "stuck".
When was the last time you felt stuck doing some mathematics and how willing were you to share that feeling, or the few ideas you had about what to do, with others? What does it mean to a problem solver to be stuck? In order to attempt to answer this question, before you read any further, you might like to try the following problem called Nine-pin Triangles which asks how many different triangles you can make on a circular pegboard that has nine pegs.
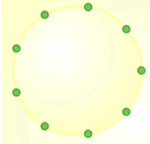
As you worked on this problem, were there any times when you felt stuck? What exactly were you stuck on? Were you able to start the problem immediately? Did you want clarification of anything at any stage? Did you feel as if you reached a solution which you're happy with? Why or why not? How did you reconcile any questions you had?
Your response to this last question might well depend on whether you were working alone or not. When I first tried this problem (which was inspired by the work of Geoff Faux), one of the barriers I came up against straight away was the notion of difference. What makes one triangle different to another in this context? Linked with this was the horrible feeling that there must be hundreds of
triangles! How would I know when I had found them all? I guess being stuck on this problem for me was initially about seeking reassurance to some extent. I wanted to talk to someone else about what "different" meant and then I experienced a feeling that perhaps is quite common for many of our pupils, that the problem was insurmountable because of the huge number of possibilities.
In this instance, I was in a room with colleagues so I was able to come to a satisfactory meaning of "different" in discussion with them. Although I was daunted by there being too many triangles to find, my experience of solving problems gave me the confidence to draw on strategies I believed would help - developing a system for finding the triangles one by one, for example. By working
systematically I could convince myself that I had found them all.
You might have noticed that I used the adjective "horrible" in the previous paragraph to describe how I felt. Is this a common emotion associated with being stuck? How did you feel while tackling the problem? Being stuck is usually thought of as being a negative state of affairs, and so it is, in the sense that progression seems out of reach or pointless. At first glance, it is easy to suggest
that we don't want our pupils to get stuck. Surely we shouldn't have a desire for them to be floundering as they work on mathematics? As teachers, our instinct can sometimes be to scaffold to such an extent that the children are not really thinking for themselves. We want them to succeed, to get the "right" answers, not to struggle. Or do we?
Going back to my own experience of working on the Nine-pin Triangles problem, the feelings I had as I reached a solution were altogether different to those I've described so far. There was a sense of elation and satisfaction; that somehow I'd triumphed. Would I have had these same emotions if I had known exactly what to do right from the start and there hadn't been any uncertainties? I am sure
that it was the fact I'd had to overcome difficulties in order to succeed that was the most significant contributor to my feelings of pride and pleasure.
Mason et al. (1982) suggest that it is the sense of slight unease which we experience when up against something challenging which stimulates us to think mathematically and it is this element of challenge that NRICH problems try to offer. However, when we are stuck, how long is it reasonable for us to be stuck for? And what is helpful when we are stuck? James Nottingham (2004) talks about a "pit
of uncertainty" in which children should not be frightened of finding themselves on the journey between having been asked a question and reaching an answer. He explains that we shouldn't leave our pupils in the pit unaided, but it is the support we give them to climb out of the other side which is crucial.
You might want to share the Nine-pin Triangles problem with your own class and/or colleagues, if appropriate, but in case you are teaching younger or less-experienced learners, you might like to look at Happy Halving instead. In this challenge, you are asked to split each of the shapes in half so that the two parts
are exactly the same.
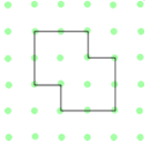
Before giving this problem to your pupils, think about how they might get stuck as they work on it. What sort of strategies could you use that encourage them to think mathematically and therefore empower them to get themselves "unstuck"? In writing hints on the website, this is exactly the process we go through.
Of course there are all manner of difficulties in trying to offer help, both in an online environment and in the classroom. Each child's relationship with a problem is different; each child's experience of solving problems is different. Therefore what is helpful to one may be useless to another. How can we try and offer support without leading our pupils down the route we would take and at the
same time leave room for there to be opportunities to find alternatives?
There is no doubt that a culture in which being stuck is valued in a meaningful way is difficult to achieve and I don't have definitive answers to my questions. However, we can model what we do when we are stuck and we can be explicit about the ways we try to help learners when they are stuck. In this way, children will begin to develop their ability to think mathematically, as Mason et al.
(1982) suggest, and therefore become more independent in their role as problem solvers. They will feel positive that a problem may be difficult but it is worth striving for a solution.
The NRICH Team always welcome your comments on the hints and notes they provide with each problem (or on any aspect of the website!). Please get in touch: primary.nrich@maths.org.uk
References
Mason, J. with Burton, L. and Stacey, K. (1982) Thinking Mathematically. Wokingham: Addison-Wesley Publishing Company
Nottingham, J. Conference keynote, Bristol 2004
This article also appears in Primary Mathematics, a journal published by The Mathematical Association.