Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Alternating Sum
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
Answer: 4015
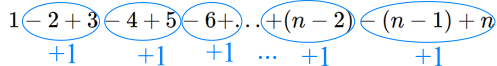
Add 1 for each odd number
$\therefore$ $n$ is the 2008th odd number
Which is 2008$\times$2$-$1 = 4015
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.