Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Rectangle Rearrangement
Age 14 to 16
ShortChallenge Level 





- Problem
- Solutions
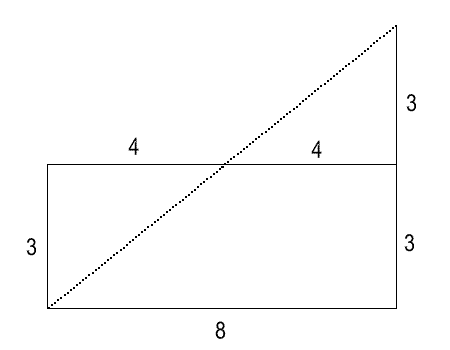
The diagram shows the two pieces will fit together to form a right-angled triangle which has a base $8$ and height $6$. The length of the hypotenuse = $\sqrt{(6^2+8^2)}$, that is $10$, so the perimeter of the triangle is $24$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.