 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Presents



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
No one has sent in a complete solution for this problem, so please send one in if you think you have it. These two partial solutions from Joanne and Jill might get you thinking!!
Joanne, West Flegg Middle School says:
I first took your plans and developed them.
After that I thought about what didn't work in the patterns and I found that groups of 4 squares together in a square didn't work:
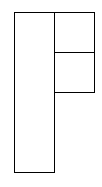

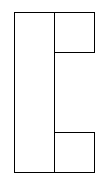
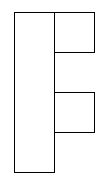
These shapes do not work
These shapes do work. They are nets of a cube:
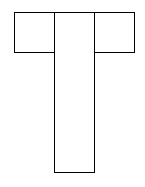
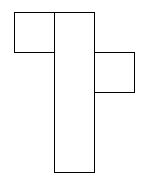
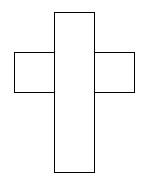
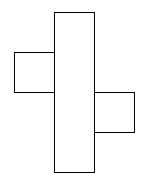
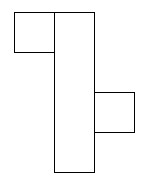
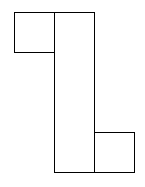
I think there are 6 different ways of covering this parcel.
Task 2: To make a net for a cuboid.
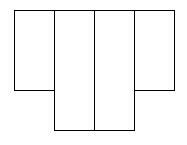
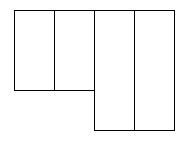
These did not work.
I found that you could not have the 2 end squares on the same side.
These are the nets that did work:
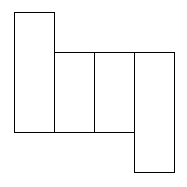
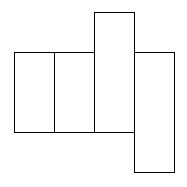
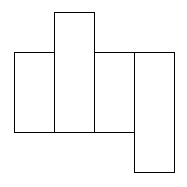
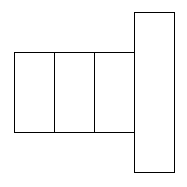
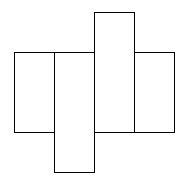
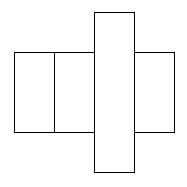
I found 6 nets that will cover this parcel.
I predict that for the present that is different from a cube in 2 directions the number of nets is 3.
Jill, also from West Flegg Middle School, says:
First of all I found several different ways of the non net (reflected, upside down, sideways). Here are two that I found the most:
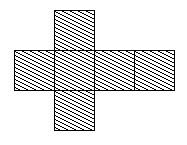
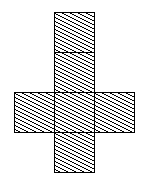
But then, when cutting out the card to test it, I cut it
wrongly.
 Then a
brainwave struck me: if I move one segment over a bit it would
work!
Then a
brainwave struck me: if I move one segment over a bit it would
work!
![]() Here are some I
investigated:
Here are some I
investigated:
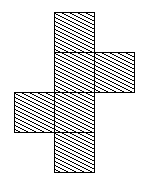
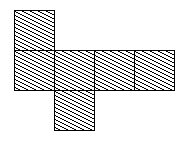
But then, when I came to this one which didn't work, I realised something: the squares that are moved have to be on the same side.
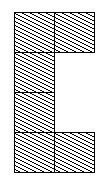
This led to some interesting thoughts:
- How many other nets can be made?
- What would happen if there weren't two squares on different
sides?
- Can we do this with other 3D shapes?
Well, the truth is there must be answers out there somewhere.