You may also like

problem icon

Just Rolling Round

P is a point on the circumference of a circle radius r which rolls, without slipping, inside a circle of radius 2r. What is the locus of P?

problem icon

Center Path

Four rods of equal length are hinged at their endpoints to form a rhombus. The diagonals meet at X. One edge is fixed, the opposite edge is allowed to move in the plane. Describe the locus of the point X and prove your assertion.

problem icon

Rolling Coins

A blue coin rolls round two yellow coins which touch. The coins are the same size. How many revolutions does the blue coin make when it rolls all the way round the yellow coins? Investigate for a line of 'n' coins

Roaming Rhombus

Stage: 4 Challenge Level: Challenge Level:1

Created with GeoGebra

 Four rods of equal lengths are hinged at their endpoints to form a rhombus ABCD.

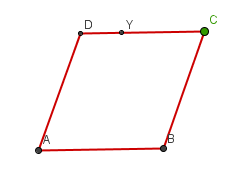
Keeping AB fixed, CD is free to move in the plane with the angle BAD between 0 and 180 degrees.

What is the locus (or path) of the point D?

What is the locus of Y, the point one third of the way along DC? (DY:YC = 1:2)

NOTES AND BACKGROUND

You might like to download your own free copy of GeoGebra from the link above and draw this dynamic diagram for yourself. You will find it easy to get started on GeoGebra with the Quickstart guide for beginners.


The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.