Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Hamiltonian Cube
Age 11 to 16
ShortChallenge Level 





- Problem
- Solutions
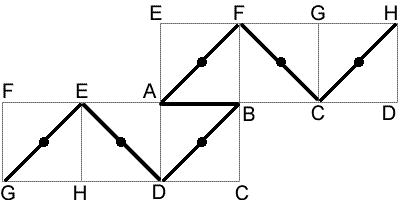
The image above shows a possible path. Each edge joining a corner to a face centre has length $\frac{1}{\sqrt{2}}$ (by Pythagoras' Theorem), while each edge which joins two adjacent corners has length $1$. So the length of the path above is $1+6\sqrt{2}$. This is the length of the shortest path to pass through all the vertices.
To prove this, note the length of the shortest path must be at least $\frac{13}{\sqrt{2}}$. Such a path would move alternately between corners and faces, but as there are $8$ corners and only $6$ faces, so this is impossible. So at least one of the edges must join to corners, and so the shortest length is $1+6\sqrt{2}$.
This problem is taken from the UKMT Mathematical Challenges.
You can find more short problems, arranged by curriculum topic, in our short problems collection.