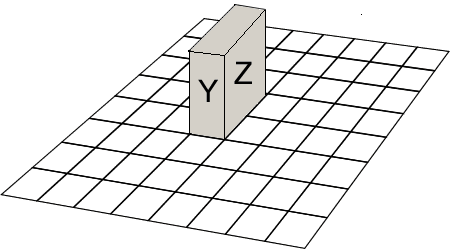
A $1\times2\times3$ block is placed on an $8\times8$ board, as shown with the $1\times2$ face $X$ at the bottom. It is rolled over an edge without slipping onto a $1\times3$ face $Y$, then onto the $2\times3$ face $Z$,then onto $X$, $Y$, $Z$ again in that order. How many different squares on the board has the block occupied altogether, including the starting and ending positions?

 

If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.

 

 

 

This problem is taken from the UKMT Mathematical Challenges.

View the previous week's solution
View the current weekly problem