 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Number Lines



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Number Lines
Leah and Tom both have number lines and a counter. They always start with their counters at zero.
Leah's number line goes along from left to right like this:

First Leah made a jump of three along her number line and then a jump of four. Where did she land?
Next Leah made a secret jump along her number line. Then she made a jump of five and landed on $9$.
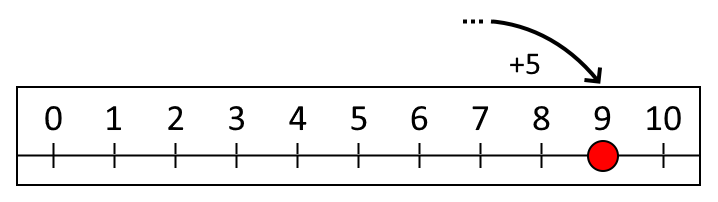
How long was her secret jump?
Then Leah made a jump of six and another secret jump. She landed on $10$.
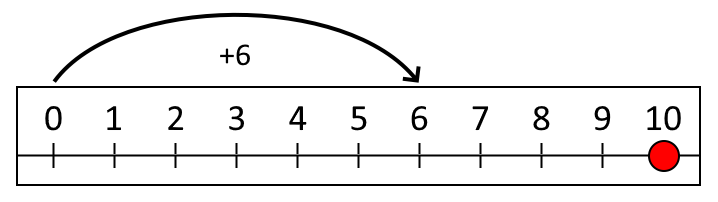
How long was her second secret jump?
Tom's number line goes up and down like this:

First Tom made a jump of three up his number line and then a jump of two. Where did he land?
Next Tom made a secret jump up his number line. Then he made a jump of six and landed on $8$.
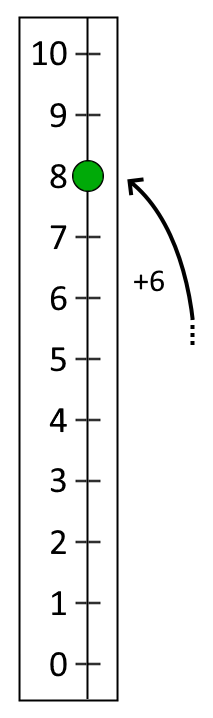
How long was his secret jump?
Then Tom made a jump of four and another secret jump. He landed on $7$.
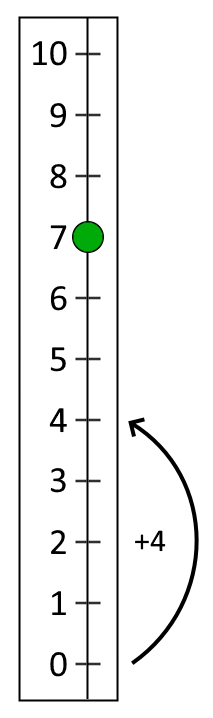
How long was his second secret jump?
There are some printable NRICH Roadshow resources for the game that this task is based on: Instructions and Number Line.
Why do this problem?
This activity is a good one to try once children are familiar with number lines, and they have begun to use them for addition. It could be a good way to talk about subtraction.
The problem requires higher-order thinking compared with simply adding or subtracting. It encourages children to be confident in "undoing" operations, and therefore introduces them to the idea of subtraction being the inverse of addition and vice versa. However, you don't need to use this vocabulary at first.
The idea of having an unknown number (the secret jump) in a calculation (further jumps along the number line) is the essence of algebra, and this problem introduces that important concept but in an appropriate context.
Possible approach
Start with a number line with which the children are familiar and then introduce a vertical number line if they have not met them before.
Involve the children in suggesting numbers to add using both number lines before introducing the idea of the 'secret jump'. Next, it might be appropriate to try some of your own examples with the group, asking them how they are going to find the secret number of jumps. Encourage pupils to explain how they will do it in their own words and discuss whether or not this will work.
Key questions
Possible extension
Use a number line which goes to up to $20$ or $100$.
Possible support
Make sure that children are counting the jumps they make, and not the starting point. If there are difficulties with a vertical number line they could focus on using a horizontal number line instead.
You may also like
Biscuit Decorations
Andrew decorated 20 biscuits to take to a party. He lined them up and put icing on every second biscuit and different decorations on other biscuits. How many biscuits weren't decorated?