Shree from the International School Frankfurt in Germany sent in these solutions in which triangles in different places were explored:

  
 

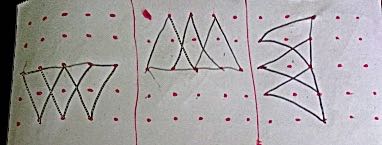
Neptune Class from Riverley Primary wrote to say:

We think that there are 6 triangles in total.

We made sure that each triangle was a different type (scalene, isosceles, right-angled and equilateral) and we experimented with different shapes on the pin-board.
We thought that there must also be a mathematical way to systematically calculate the solution to the problem, but we're still working on it.

I think there are a few more than six triangles, but I like the way you thought that working systematically would help. 

That's exactly what Greg from Swanland County Primary School did.  He said:

First I tried to just make triangles with a dot inside.

 

Then I tried ones with a four dot base.

 

Then I tried one with a two dot base.

 


I think there are 7 different triangles.
 

We had a solution come in from Lily-Mai and Dillon from Millbrook School in Swindon. Their teacher wrote to say that they think they have found all nine triangles, and would love to see their solution on the NRICH website! We agree with Lily-Mai and Dillon - there are nine different triangles. They worked systematically, finding all triangles with a base of 2, then 3, then 4:

These show some very good approaches.  Thank you for sending them into us.

Some of you might like to explore further, being curious about what having two dots within the triangles would be like, for example.