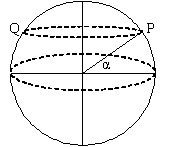To solve this problem we shall consider that the point is situated at latitude $\alpha$. To travel around the line of latitude, the distance from P to Q would be half the circumference of the circle at latitude $\alpha$. This circle has a radius $R \cos \alpha$, where $R$ is the radius of Earth.

So, the distance traveled from P to Q on the line of latitude is $d_{lat} = \pi R \cos \alpha$.

Traveling over the line of longitude, the circle on which we have to calculate the distance is a great circle of the sphere, and the angle of displacement is $2(\pi /2 - \alpha)$ radians. The distance is therefore $4\pi R(90-L)/360$ where $L$ is the angle of latitude in degrees or equivalently $d_{long} = 2R (\pi/2 - \alpha)$.

It is clear that the path on a great circle is always shorter.

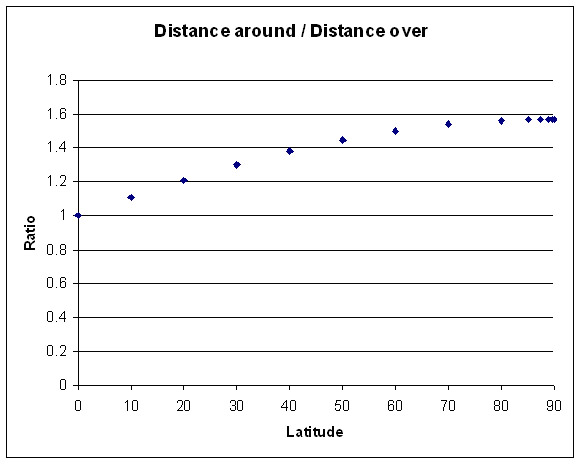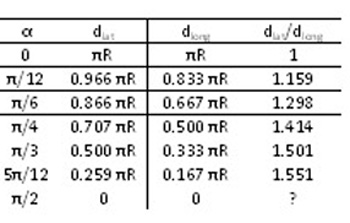
A graph of the ratio of these distances shows that this ratio seems to tend to $\pi /2$ as the line of latitude approaches the pole, that is the ratio $${d_{lat}\over d_{long}}= {\pi R \cos \alpha \over 2R (\pi/2 - \alpha)}$$ tends to a limit as $\alpha \to \pi/2$.

This ratio can also be written as $${d_{lat}\over d_{long}}= {\pi R \sin (\pi/2- \alpha) \over 2R (\pi/2 - \alpha)}.$$ As we know ${\theta\over \sin \theta} \to 1 $ as $\theta \to 0$ we can take $\theta = \pi/2 - \alpha $ and we see that this limit is $\pi /2$.