How Many Geometries Are There?

An account of how axioms underpin geometry and how by changing one axiom we get an entirely different geometry.

When the Angles of a Triangle Don't Add up to 180 Degrees

This article outlines the underlying axioms of spherical geometry giving a simple proof that the sum of the angles of a triangle on the surface of a unit sphere is equal to pi plus the area of the triangle.

Flight Path

Use simple trigonometry to calculate the distance along the flight path from London to Sydney.

Over the Pole

Stage: 5 Challenge Level:

Simon from Elizabeth College, Guernsey and Andrei from Tudor Vianu National College, Romania have both solved this problem and both solutions are used below.

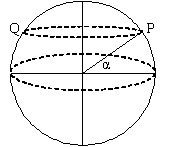To solve this problem we shall consider that the point is situated at latitude $\alpha$. To travel around the line of latitude, the distance from P to Q would be half the circumference of the circle at latitude $\alpha$. This circle has a radius $R \cos \alpha$, where $R$ is the radius of Earth.

So, the distance traveled from P to Q on the line of latitude is $d_{lat} = \pi R \cos \alpha$.

Traveling over the line of longitude, the circle on which we have to calculate the distance is a great circle of the sphere, and the angle of displacement is $2(\pi /2 - \alpha)$ radians. The distance is therefore $4\pi R(90-L)/360$ where $L$ is the angle of latitude in degrees or equivalently $d_{long} = 2R (\pi/2 - \alpha)$.

It is clear that the path on a great circle is always shorter.

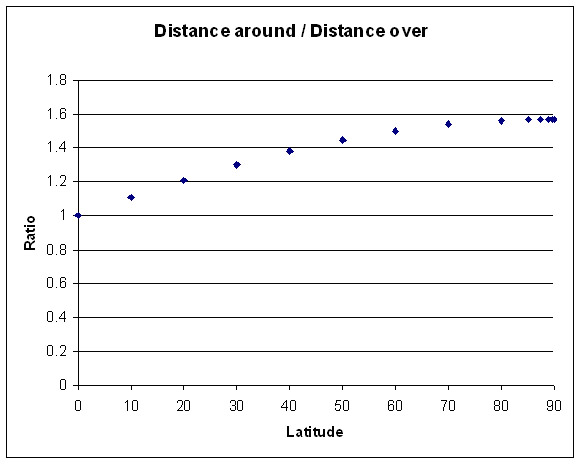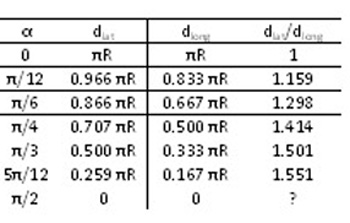
A graph of the ratio of these distances shows that this ratio seems to tend to $\pi /2$ as the line of latitude approaches the pole, that is the ratio $${d_{lat}\over d_{long}}= {\pi R \cos \alpha \over 2R (\pi/2 - \alpha)}$$ tends to a limit as $\alpha \to \pi/2$.

This ratio can also be written as $${d_{lat}\over d_{long}}= {\pi R \sin (\pi/2- \alpha) \over 2R (\pi/2 - \alpha)}.$$ As we know ${\theta\over \sin \theta} \to 1 $ as $\theta \to 0$ we can take $\theta = \pi/2 - \alpha $ and we see that this limit is $\pi /2$.

Andrei calculated this limit using L'Hopital's Rule (case $0/0$): $$\lim_{\alpha\to \pi/2}{\pi R\cos \alpha \over R(\pi -2\alpha)} = \lim_{\alpha\to \pi/2}{\pi \cos \alpha \over (\pi -2\alpha)} = \lim_{\alpha\to \pi/2}{-\pi \sin \alpha \over -2} = {\pi \over 2} \approx 1.57$$

Spheres. Cosine. Complex numbers. Non Euclidean Geometry. Limits. Mathematical reasoning & proof. Tangent. Sine. Circumferences. Geodesics.

You may also like

How Many Geometries Are There?

When the Angles of a Triangle Don't Add up to 180 Degrees

Flight Path

Over the Pole

Stage: 5 Challenge Level: