Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
A Scale for the Solar System
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
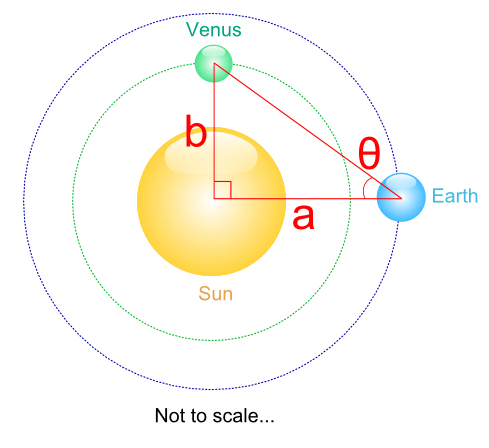
Lukaz Smith, from Parkside School, sent in the following correct approach to finding the ratio of the Earth-Sun and Venus-Sun distances (diagram added to help clarify the solution)
If you said the Earth to sun distance was 1 astronomical unit ($a$ in diagram), then you could simply measure the angle ($\theta$ in diagram) between Sun, Earth and Venus, when you knew that there was a 90 degree angle between Earth, Sun and Venus. Then you just find the tangent of the angle, so it's 1 : $\tan \theta$ as the ratio of Earth to Sun distance and Venus to Sun distance.