Quaternions and Rotations

'Quaternions and Rotations' printed from https://nrich.maths.org/

Show menu

Andrei from Romania sent in a good solution to this problem.

(1)(a) We have to show that $qq^{-1} = 1$: $$q^{-1} = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i}) = {1\over 2}(1 - {\bf i}^2) = 1$$ (b)Take $x = ti$ to be any point on the x-axis. Then $qx = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t{\bf i} = {-1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})t = xq.$

We have shown that $qx = xq$ and so $qxq^{-1} = x$.

Let $F(v) = qvq^{-1}$ be a mapping of points $v$ in $R^3$ to images in $R^3$ where the 4-dimensional quaternion $q$ acts as an operator. We have proved that this mapping fixes every point on the x axis.

(c)What effect does this mapping have on other points in $R^3$? $$F({\bf j})= qjq^{-1} = ({1\over \sqrt 2} + {1\over \sqrt 2}{\bf i})({\bf j}) ({1\over \sqrt 2} - {1\over \sqrt 2}{\bf i})$$ $$ = {1\over 2}(1+{\bf i})({\bf j})((1 - {\bf i})$$ $$ = {1\over 2}({\bf j} + {\bf k})(1 - {\bf i})$$ $$ = {1\over 2}({\bf j} + {\bf k} + {\bf k} - {\bf j})$$ $$= {\bf k}.$$ Similarly $F{\bf k} = -{\bf j}$. Parts (b) and (c) together show that the mapping $F(v) = qvq^{-1}$, where $q = \cos (\pi /4) + \sin (\pi /4) {\bf i}$, gives a rotation of $\pi /2$ about the x axis.

(2) In this section we consider the mapping $G(v) = qvq^{-1}$ of $R^3$ to $R^3$ where the quaternion $q = \cos \theta + \sin \theta {\bf k}$ is an operator.

(a) $(cos \theta + \sin\theta k)(\cos \theta - \sin \theta k) = \cos^2 \theta + \sin^2 \theta = 1$ so these two quaternions are multiplicative inverses.

(b) We have $qk = -\sin \theta + \cos \theta k = kq$ and hence $qkq^{-1} = k$. So the mapping $G(v) = qvq^{-1}$ fixes the z-axis.

(c) What effect does the mapping $G$ have on vectors in $R^3$? We consider the vector $v = r(\cos \phi {\bf i} + \sin \phi {\bf j})$. $$ qvq^{-1} =(\cos \theta + \sin \theta {\bf k})r(\cos \phi {\bf i} + \sin \phi {\bf j}) (\cos \theta - \sin \theta {\bf k}) $$ $$= r((\cos \theta\cos \phi - \sin \theta \sin \phi){\bf i} +(\cos \theta \sin \phi + \sin \theta \cos \phi){\bf j}) \cos \theta {\bf i} -\sin \theta {\bf k}) $$ $$ = r(\cos (\theta + \phi) {\bf i} + \sin (\theta + \phi){\bf j}) (\cos \theta {\bf i} -\sin \theta {\bf k}) $$ $$= r((\cos (\theta +\phi)\cos \theta - \sin (\theta + \phi)\sin \phi){\bf i} + (\cos (\theta +\phi)\sin \theta + \sin (\theta + \phi)\cos phi){\bf j})$$ $$= r(\cos (2\theta + \phi){\bf i} + \sin (2\theta + \phi){\bf j}).$$

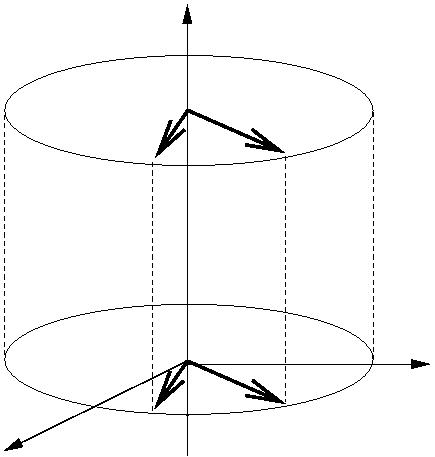We have shown $qkq^{-1} = k$ so $G(v+tk)= q(v +tk)q^{-1} = qvq^{-1} + qtkq^{-1} = qvq^{-1} + tk$ for all $t$.

We can see that the vector $v$ in the $xy$ plane is rotated about the $z$ axis by an angle $2\theta$ and all points on the vertical line through it are also rotated about the $z$-axis by an angle $2\theta$.

So by the mapping $G(v) = qvq^{-1}$ all points in $R^3$ are rotated by $2\theta$ about the $z$-axis.

Note that, for any rotation of $R^3$, we can make a transformation of the coordinate system so that the axis of the rotation is made to coincide with the $z$-axis, then perform the rotation by the given angle about the $z$-axis, and finally transform back to the original coordinate system.