Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
How Does Your Function Grow?
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Here are two solutions, one from Simon from Elizabeth College, Guernsey and one from Andrei from Tudor Vianu National College, Bucharest, Romania. First Simon's solution.
The functions are: $$\eqalign { A(n) &= \log(100n) \cr B(n) &= n^{100} \cr C(n) &= 100^n \cr D(n) &= n! .}$$ Firstly I looked at Archimedes' choice, the logarithmic function. $$A(n) = \log(100n) = \log 100 + \log n.$$ I knew that when $n$ gets large $\log 100$ would become irrelevant. This meant that only $\log n$ would be important, and $\log n < n$ when $n > 1$. So $A(n)$ will be less than $n$ for large $n$. We find $n = \log(100)+ \log n$ for $n = 6.472775$ approximately and so $A(n) < n$ for all values of $n> 6.5$.\par The next task was establish whether $B(n)$ or $C(n)$ was greater for large numbers. I was certain of one thing: $B(n) = C(n) = 100^{100}$ for $n=100$.
Firstly I knew that $100^n$ would have $2n+1$ digits. I then established, where $x$ is the number of digits in $n$, that $n^{100}$ would have between $100(x-1)+1$ and $100x$ digits. So $C(n) = 100^n$ is the larger function for $n> 100$.
Therefore, so far, $C(n)$ is the largest function for large values of $n$.
The next task was to compare it to $D(n)$ or factorial $n$.
Using Stirling's formula: $$D(n) = n! = \sqrt{2\pi n} ({n\over e})^n.$$ As $n$ is a large positive number, $\sqrt {2\pi n}$ will be greater than 1. Therefore when ${n\over e}$ is greater than 100, $D(n) > C(n)$. The 'change over point' occurs for $n$ just less than $n = 100e$, that is $ n \approx 270$.
Andrei considered the natural logarithms of the functions and plotted their graphs. For the factorial n function Andrei used Stirling's Approximation which is valid for large n.
I approximated the function for factorial n further by
ignoring the term $\sqrt{2\pi n}$. $$\eqalign{ A(x)&= \log (n)
+ \log(100) \cr \log(B(n)) &= 100 \log(n)\cr \log C(n) &= n
\log(100) \cr \log D(n)&\approx n\log(n) - n }.$$ I know that
$log(n)< n$ for the whole domain of definition of the
logarithmic function, and I see that $A$ is the smallest. I have to
compare the other functions. As $ \log(100)\approx 4.60$, so:
$$\eqalign { \log(B) &= 100 \log(n) \cr \log(C)&\approx
4.6n \cr \log(D) &\approx n (\log(n) -1).}$$ In the limit for
large $n$, $$ \lim_{n\to \infty}{\log n\over n}\to 0$$ and so
$B< C$.
For large $n$ we can neglect 1 in respect to $\log(n)$ in the
approximate formula for $\log(D)$ and, as $4.6 < \log (n)$ we
have $D> C> B> A$.
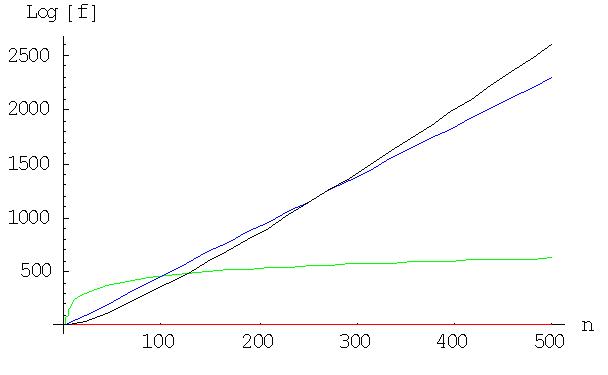
Here in the diagram, $A(x)$ is represented in red, $B(x)$ in
green, $C(x)$ in blue and $D(x)$ in black. It can be observed that
for large $n$ (here $n> 300$) the order of the magnitude of the
functions is $D> C> B> A$.