Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Dotty Circle
Age 7 to 11
Challenge Level 





Watch the film below.
Try to describe what happens in the film to someone else.
Imagine the dot starts at the point (1,0), turns through $20^\circ$ and then stops:
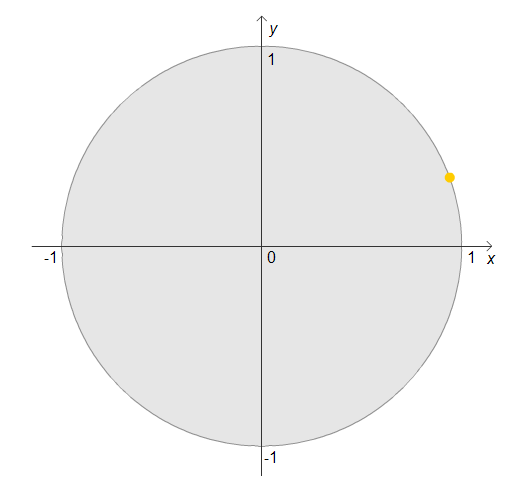
If the point now carries on, through how many degrees must it turn to finish the same height above or below the horizontal axis as it was when it had gone through $20^\circ$?
Can you find a general rule for explaining when the dot will be this same distance from the horizontal axis?
You might like to try Round and Round and Round after this problem.