 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Method in Multiplying Madness?



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Thank you to everyone who sent in their thoughts about these different methods. We were very impressed by your efforts to compare the different methods, especially how you thought carefully about their advantages and disadvantages, perhaps even including the number of steps you needed to reach an answer.
Tylar, from St Michael's International School in Japan, shared his thoughts about the advantages and disadvantages of the four different methods in this table:
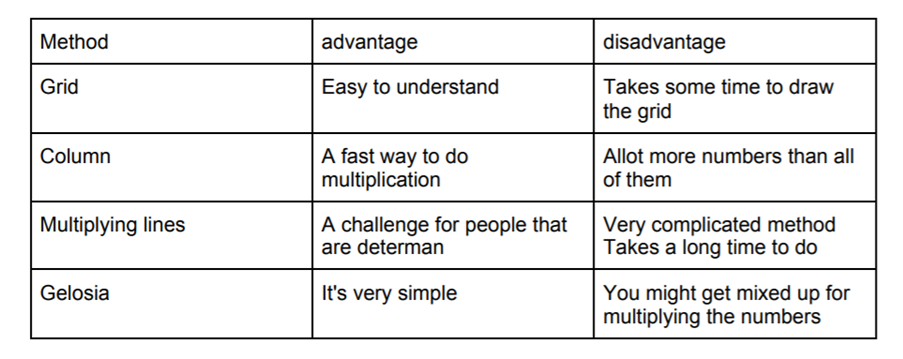
Thank you, Tylar.
Of course, not everyone works in the same way. An approach that seems easy to understand for one person can appear to be much harder for someone else. Do you agree with Tylar's comments about each approach? Are there any you disagree with?
Eira, from Twyford School, also shared her thoughts about the different methods as well as some photos of her working out. Here are her comments on the grid method:
For this method to work you have to partition the numbers that you are working with. For example, 31 x 13, if you partition both of those numbers then the calculation looks easier and more approachable. This is exactly the same as column multiplication. The only difference is that grid multiplication is... on a grid!
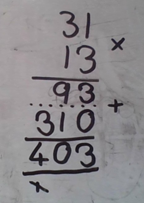
Eira suggested that the grid and column methods are very similar. Do you agree? Here are Eria's thoughts about the column method:
This can be very useful for certain numbers but not for others. This is very similar to grid multiplication. It is partitioning the numbers as well, just not showing it. The most important thing is that you have to remember to write the 0 in the second line otherwise the method will not work.
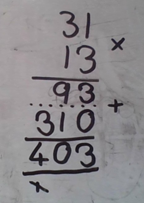
Although multiplying by lines looked very different from the grid and column methods, many of you told us that it can be easy and fun too. Here are Eria's thoughts after learning how to use this approach:
Multiplying with Lines: This is a really clever method. It is also very simple, once you get to know it. To do it you have to draw out lines for each of the digits of the two numbers, see the picture below. Then you have to draw two dotted lines, as shown, separating the bottom corner from the middle two corners and the top corner from them as well. After this you have to add up all of the places where the lines are perpendicular and make a corner. But you must remember to only add them up on their side of the dotted lines. The numbers that you get are the digits of your product, shown in the order below.

Thank you, Eria. The fourth multiplication method which we shared with you was the Gelosia approach. Eria tried out this approach too, comparing it with the grid and multiplying by lines methods:
Gelosia Multiplication: This is set out in a sort of grid, only slightly different to grid multiplication. Unlike grid multiplication this method doesn't partition the numbers, it only takes the digits and puts them in the correct spaces. You then need to times the numbers like you do in grid multiplication and write them in the boxes. The diagonal block lines are only for if you have a two-digit number as your answers in the boxes. Then write in the dotted diagonal lines and add up the numbers on their side of the dotted lines. Wait, that's rather like multiplying with lines! Again, as you can see in the picture the 10 that you get from adding 9 to 1 has to be split up and the 1 has to be added to the 3.

Which method do you prefer? When you've completed a calculation, it can be useful to check your answer using another method. Which one might you choose?
You may also like
Exploring Wild & Wonderful Number Patterns
EWWNP means Exploring Wild and Wonderful Number Patterns Created by Yourself! Investigate what happens if we create number patterns using some simple rules.
Pebbles
Place four pebbles on the sand in the form of a square. Keep adding as few pebbles as necessary to double the area. How many extra pebbles are added each time?