Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Perpendicular Lines
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We received correct solutions from Ash and
Lucy, two students at Tiffin Girls' School. Well done to you
both.
Ash sent us this correct solution:
The gradient of the first line must be the negative reciprocal
of the gradient of the other line:
if you multiply the two gradients you always get -1.
For example:
Take a random gradient, say $\frac{4}{7}$
The negative reciprocal gradient will be $\frac{-7}{4}$
Make up two equations with these gradients, say
$y =\frac{4x}{7}$ and $y =\frac{-7x}{4}$
Draw them on a grid
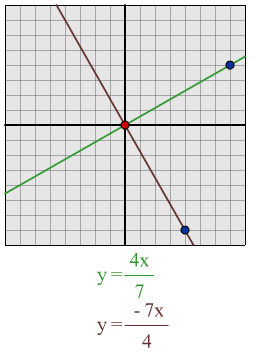
You get perpendicular lines.
Lucy recorded how she worked through this
problem:
$y = x$ is perpendicular to $y = -x + 2$
(the y-intercept doesn't affect the
gradient of the line)
$y = 2x$ is perpendicular to $y = -x/2$
$y = -3x$ is perpendicular to $y = x/3 $
(to make a line perpendicular you
need to invert the gradient, or take the reciprocal, and change the
sign)
$y = -2x$ is perpendicular to $y = x/2 $
I can see a pattern here: when the two gradients of perpendicular lines are multiplied together they give -1, and the y-intercept does not affect if the line is perpendicular or not.
I will now try to work out what the perpendicular line of some other lines will be using this formula:
$y = 7x - 3$:
Using my formula I predict that a line which is perpendicular to this line will be $y = -x/7 - 3$
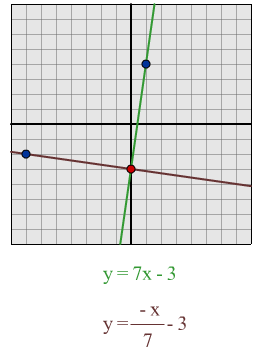
When I tested the lines out, I found that the formula had worked.
$y = x/3 + 4$:
Using my formula I predict that a line which is perpendicular to this line will be $y = -3x + 4$
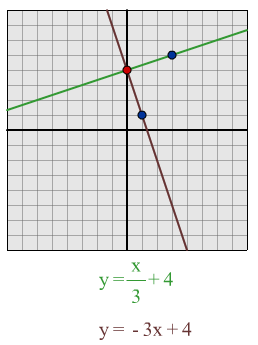
Having drawn out the lines I found that the formula worked and the lines were perpendicular.
$y = -7x/3 + 2$:
I predict that a line which is perpendicular to this line will be $y = 3x/7$
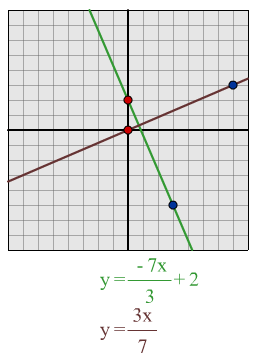
From drawing out these lines I can see that they are perpendicular.
You may also like
Intersections
Change one equation in this pair of simultaneous equations very slightly and there is a big change in the solution. Why?
