 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
From All Corners



- Problem
- Student Solutions
The answer 1/6 was found in a rich variety of ways, but what is really important is not the answer but proving it.
Kathy, Sarah, Alice, Clare, Jenny, Anna, Tam, Claire and their mates in year 10, from the Mount School, York (I hope no-one has been left out) found that there were some triangles that are similar. They had begun "by trying to draw it accurately, using different sizes of square, and those of us who began with a square of side 12 cm arrived at the answer first, because the points all land on easy grid points and the numbers are easy. We then worked back trying to prove/convince ourselves of what we were assuming!".
This group knew that, to make this a really good solution they would have to explain why the vertices of the octagon lie on 'easy' grid points, and they knew the reasons were to do with similar triangles.
Here is the diagram drawn by Amy of Madras College . Her diagram shows clearly that the octagon has an area of 24 square units and the large square an area of 144 square units. Amy gave a good account of how she worked out the answer, but again she assumed, but did not prove, that the vertices of the octagon were exactly on those easy grid points. No-one can know that just from drawing!
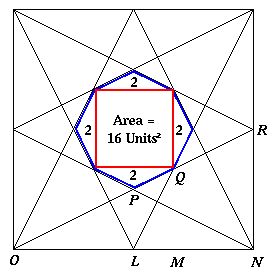
For ease of labelling we use co-ordinates, taking O as (0,0) and N as (12,0). By symmetry L is (6,0) and R is (12,6). What about P and Q ? Are they exactly where we have assumed them to be?
From the gradient of the line O R , or the fact that triangles O P L and O R N are similar, it follows that P L = 1/2 R N which proves that the coordinates of P are (6,3).
By symmetry Q is on the diagonal of the square and Q M = M N . Again either from the gradient of the line O R , or the fact that triangles O Q M and O R N are similar we know that O M =2 Q M and putting these two results together we have O M =2 M N so M is the point (8,0) and Q is the point (8,4).
The shortest communique, but without proof, was from Laura, Charlotte and Laura of Maidstone Girls' Grammar School . They wrote:
| "Using trigonometry, the sine rule and area of a triangle=1/2 ab sinC, the ratio of the area of the octagon to the square is 1:6" |