Students from Ms White's Yr 7 maths class in Lyneham High School, Australia, noticed that:

Every time you go down 5 degrees in the Celsius scale, you go down 9 degrees in the Fahrenheit scale.

0 ºC = 32 ºF

-5 ºC = 32 ºF - 9 = 23 ºF

-10 ºC = 23 ºF - 9 = 14 ºF

-15 ºC = 14 ºF - 9 = 5 ºF

-20 ºC = 5 ºF - 9 = -4 ºF

-25 ºC = -4 ºF - 9 = -13 ºF

-30 ºC = -13 ºF - 9 = -22 ºF

-35 ºC = -22 ºF - 9 = -31 ºF

-40 ºC = -31 ºF - 9 = -40 ºF

-40 ºC = -40 ºF

  

They described a way of converting Celsius readings into Fahrenheit:

We know 0 degrees Celsius = 32 degrees Fahrenheit.

And an interval of 1 degree Celsius = 1.8 degrees Fahrenheit.

So, for example, if you want 5 degrees Celsius, you have to times 1.8 by 5 and then add 32.

C x 1.8 + 32 = F

 

And then rearranged this formula to convert Fahrenheit into Cesius:

You can reverse the equation above and say

(F - 32) ÷ 1.8 = C 

 

This is how they found a temperature at which the Fahrenheit reading is 20 degrees higher than the Celsius reading:

C x 1.8 + 32 = F and F = C + 20

C x 1.8 + 32 = C + 20

32 + 0.8 C = 20

0.8 C = -12

C = -15

F = 5  

 

Nina, Kristjan and Jure from the Elementary School in Loka Crnomelj in Slovenia sent us this most comprehensive solution, explaining clearly all stages of their work.

Many students knew the formula for converting Celsius into Fahrenheit and used this to find the temperature at which the Celsius and Fahrenheit readings are the same.

Here are the three strategies that Michael from Bilton School used to find the temperature.

This is how Samuel from Long Buckby Junior School reasoned:

There is a temperature at which Celsius and Farenheit are the same.

It is $-40$ degrees, because $9/5$ of $-40$ is $-72$ and $-72 + 32 = -40$.

I decided to look at negative numbers because starting with a positive number and multiplying it by $9/5$ is going to increase it and so is adding 32 so you're always going to end up with a number greater than the number you started with.

However, if you start with a negative number, multiplying it by $9/5$ decreases it, and adding $32$ increases it, so I realised that with the correct number, Celsius and Fahrenheit might be the same.

I decided to go down in tens:

$9/5$ of $-10 = -18$

and $-18 + 32 = 14$,

so that doesn't work;

$9/5$ of $-20 = -36$

and $-36 + 32 = -4$,

so that doesn't work;

$9/5$ of $-30 = -54$

and $-54 + 32 = -22$,

so that doesn't work.

But $9/5$ of $-40 = -72$

and $-72 + 32 = -40$ so it works.

The reason it works is because multiplying by $9/5$ is equivalent to adding $4/5$ of it, and for $-40$ adding $32$ is equivalent to subtracting $4/5$ of it (because $32$ is $4/5$ of $40$).

Because of this, Farenheit and Celsius are equivalent ONLY at $-40$ degrees.

The Four Mathemateers from Brocks Hill Primary School also used a trial and error approach, as displayed here:

First we started going down in tens of Celsius from $0$, and we found out a pattern:

the difference between F and C was getting closer by eights every time.

When we got to $-30C$ the difference was only $8$. So $-30$C is equal to $-22$F.

Then we tried $-40$C and found out that $-40$C was the same as $-40$F.

So the answer is $-40$.

 

Yesuhei used a similar strategy:

Others who found the correct answer by this method are Emma and Chloe from The Mount School and Michael from Bilton School.

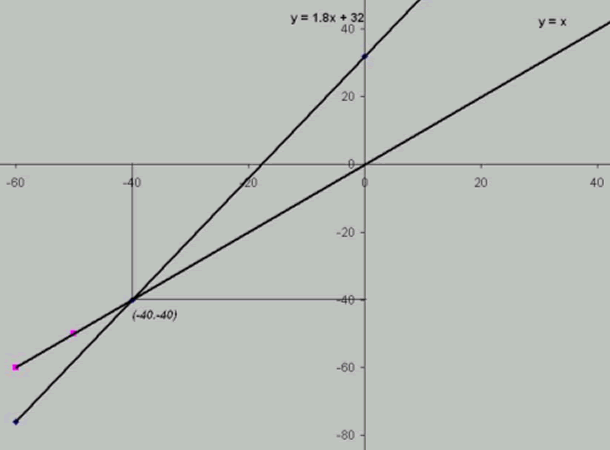
Beatrice fron Raffles Girls' School and Michael used a graphical approach.

Michael's answer is shown here:

I plotted the lines of the simultaneous equations against each other and found where they crossed.

In the graphs $y =$ F and $x = $C.

 

Image

The quickest way to solve this problem is with an algebraic approach, and both of the people who used graphs used this approach as well. The other people that obtained the correct answer by this method include Vyas from Wilson's School, Patrick from Woodbridge School, Sugam and Fiona from The Mount School, Chris from CCSN, Samantha from The Steele School, Gemma, Griselda and Charlie from Colyton Grammar School, Jasvir, Matt and Christian from Kingshill, Ed from Tunbridge Wells Grammar School for Boys, Stephen and Joe from Singapore International School, Kieran from Alcester Grammar School and Pradeesha.

Here is the solution from Vyas:

F = 9C/5 + 32 

When C = F

C = 9C/5 + 32

5C = 9C + 160

4C = -160

C = -40 

 

Here is how Patrick solved the problem:

Since F = (9C/5) + 32

then F = 9F/5 + 32

therefore F - 32 = 9F/5

5F - 160 = 9F

4F = -160

F = -40

To check: -40 = [(9 x -40) / 5] + 32

-40 = (-360 / 5) + 32

-40 = -72 + 32

-40 = -40

QED  

 

Here is Sugam's working:

 

Let x be the temperature where Fahranheit and Celsius are equal.

$x=\frac{9}{5} x+32$

$5x = 9x + 160 $

$-4x = 160 $

$x = -40 $

Therefore $-40$ Celsius $= -40$ Farenheit

And here is Michael's solution:

To solve it algebraically I can create two simultaneous equations:

$F = C$

$F = 1.8C + 32 $

Therefore

$C = 1.8C + 32 $

$C = -32 / 0.8 = -40 $

And here is Kieran's solution:

Using the equation, $F=\frac{9}{5} C+32$,

we can remove the fraction by multiplying both sides by five.

Doing so produces $5F = 9C + 160$, and thus, using the sought after equation of $F = C$,

we may further deduce that, since $5F$ and $5C$ are one and the same, subtracting the two equal amounts from either side leaves

$0 = 4C + 160$

or $4C = -160$

or $C = -40$

Consequently, $-40$ Celcius is the same as $-40$ Fahrenheit.

Oliver remembered to check that his solution worked:

We can substitute $-40$ as $C$ in $F = 9/5C + 32$ to check our answer

As $-40 = -72 + 32$, our answer is correct

Beatrice combined an algebraic and graphical approach:

 

This is a linear equation, because it follow the structure $y = mx + c$

Now let us make C the subject:

$F = (9/5)C + 32 $

$F - 32 = (9/5)C$

$C = (5/9)(F - 32)$ [equation 2]

Now plot equations 1and 2 on Graphmatica.

They will intersect at the point $(-40,-40)$.

So we know that $-40F = -40C$.

 

Image

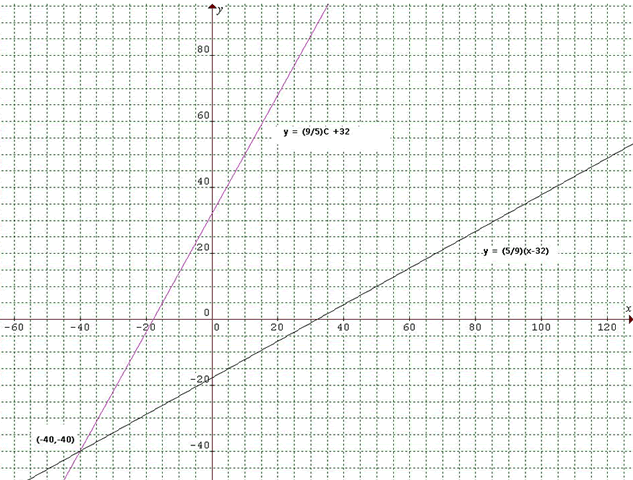
Patrick from Otterbourne was interested in finding temperatures at which readings are the same, for Celsius and Fahrenheit, Kelvin and Celsius, and Fahrenheit and Kelvin. Here is his solution.

Alexander from Wilson's School was interested in finding how to convert Celsius and Fahrenheit readings into Kelvin:

A good way of converting Celsius into Kelvin is to just add 273.15 to Celsius and you will get Kelvin. This is how I worked it out:

Celsius temperatures:

Freezing: 0C

Boiling: 100C.

Total gap: 100.

Kelvin temperatures:

Freezing: 273.15K

Boiling: 373.15K

Total gap: 100.

Therefore, because the gap is the same, you just have to add 273.15 to the Celsius temperature to get Kelvin, and vice-versa.

To convert Fahrenheit into Kelvin you need to do the following equation:

Kelvin = [(Fahrenheit - 32) x 5/9] + 273.15

The way I found this was that I did the formula from Fahrenheit into Celsius and added 273.15 to the end. 

Vatsal, also from Wilson's School, worked on finding temperatures at which the Celsius and Fahrenheit readings differed by 20:

 

The formula to change Farenheit (F) into Celcius (C) is: F = 9C/5 + 32

To find at what temperature Farenheit and Celcius are the same, you would do this:

F = 9F/5 + 32 

 

To find at what temperature Farenheit is 20 higher than Celcius, you would do this:

F = 9(F - 20)/5 + 32

F = (9F - 180)/5 + 32

F - 32 = (9F - 180)/5

5F - 160 = 9F - 180

-4F= -20

F = 5

This tells us that 5 degrees Farenheit is the same as -15 degrees Celcius.

To find at what temperature Celcius is 20 higher than Farenheit, you would do this:

C - 20 = 9C/5 + 32 

  

Niharika from Leicester High School for Girls sent us this comprehensive solution to all the different questions in the problem.

Well done to all of you who contributed solutions to this problem.