Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Flight Path
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
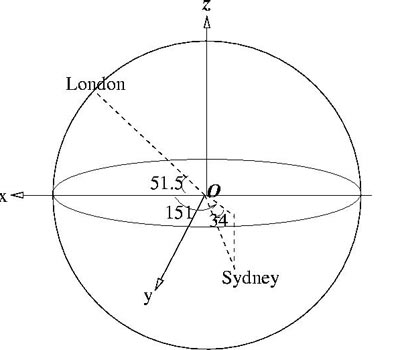 |
You need to show that if a place has (latitude, longitude) = $(p,q)$ then its coordinates are $$(R \cos p \cos q, R \cos p \sin q, R \sin p).$$ |
 |
Steps in the
calculation
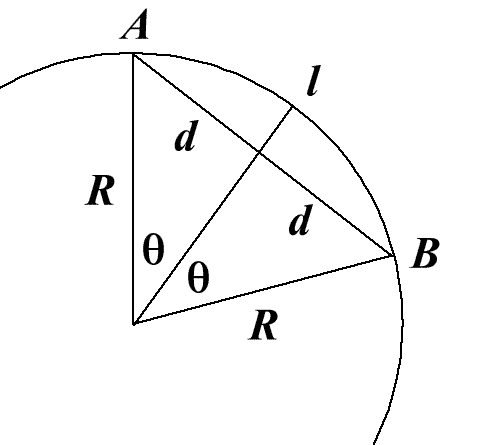
We need the distance $l$ on the surface between A and B.
First calculate the three-dimensional coordinates of A and B
from the latitude and longitude of the two points.
Then calculate the distance $2d$ (imagine a tunnel straight
through the earth from A to B) using Pythagoras Theorem.
Use $R$, the radius of the Earth, and $d$ to find the angle
$\theta$ radians where $$\sin \theta = {d\over R}.$$ Calculate the
arc length $l$.
|