A story about absolutely nothing
I remember learning this rhyme as a child. Do you know it? It was probably one of the first times I thought about nothing, and it did its job in confusing me!
'As I was going up the stair
I met a man who wasn't there.
He wasn't there again today,
I wish, I wish he'd stay away.'
But most of us seem perfectly familiar with what seems to be an easy to understand idea. Surely it is not difficult if we use it so much in our everyday language.. For example;
- 'Let's zero in on'
- 'It's nothing to do with me.'
- 'There is nothing new in this world.'
- 'Nothing's changed.'
- 'Nothing ventured nothing gained.'
- 'He was nothing to me.'
Can you think of other phrases you have used, or heard, that refer to "nothing" or "zero"?
From the Stars
More than 12,000 years ago humans spent a great deal of their time hunting for food and harvesting from the plants around them. All they ate they had to hunt for or gather from the wild. They did not keep their own cattle or grow their own food. But, between 7,000 to 12,000 years ago mankind began to settle in small communities. They began to farm and raise herds.Then, about 5000 years ago those small communities began to organise themselves and this was the beginning of civilisation as we know it today. Because people stayed in the same place and farmed they had more time to think and observe what was around them and one of the most important things they needed to know about was how to measure time and know where in the annual cycle they were. When would it be best to plant crops or to expect rain in dry climates? They began to use the phases of the sun, moon and stars to help them keep track of time. For example, the Egyptians were able to tell when the Nile was due to flood by studying the dog star (Sirius). Time was central to the cycle of life so it was crucial to be able to 'control' the calendar. They needed symbols to count the days and phases of the moon and to communicate with others.
The Purpose of Numbers
To start with people could only count the cattle they had or the days using tallying systems.How do you represent a tally? I suspect it is similar to my tallying:
![]()
Tallies are rather long-winded, especially for large numbers and ancient civilisations came up with more efficient ways of recording numbers. For example, the Egyptians used Hieroglyphs but there were other pictorial systems too.
Pictorial systems are all very well but they do not make calculation, even adding, easy. Systems were needed that would support calculation.
A Reminder - Base 10
We count and calculate in base 10. In base ten we have nine digits plus zero and this is all we need to write any number.For example:
|
$6$
|
$2$
|
$7$
|
$3$
|
|||
|
$6$ x $1000$
|
+
|
$2$ x $100$
|
+
|
$7$ x $10$
|
+
|
$3$ x $1$
|
|
$6$ x $10$ x $10$ x $10$
|
+
|
$2$ x $10$ x $10$
|
+
|
$7$ x $10$
|
+
|
$3$ x $1$
|
|
$6$ x $10^3$
|
+
|
$2$ x $10^2$
|
+
|
$7$ x $10^1$
|
+
|
$3$ x $10^0$
|
The 'Base' does not have to be 10, it could be 20 or we could use base 16 or even base 60... So, how did we end up where we are today?
Pictorial Representations of numbers
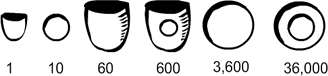
Hieroglyphs were being used by the Egyptians in 3000 BC

Using the hieroglyphs we know that:
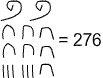
Here is one for you to try (answer at the end of the article):
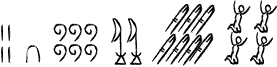
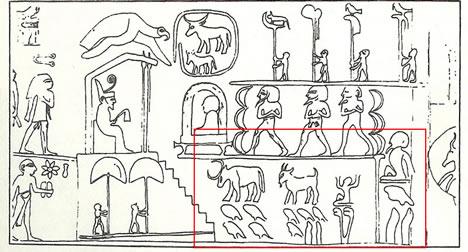
Here are some hieroglyphs on King Narmer's War Club (about 3000 BC). Along the bottom, and outlined in red, the hieroglyphs tell how many bulls, goats and human prisoners the king took. Can you work it out?
Notice that the pictures or hieroglyphs can be written in any position - you know what they are worth by their shape.
In Babylon
Around 2600BC the Babylonians were using a system similar to the Egyptians but theirs was based on 10 and 60:
Later, and very importantly, they introduced what is known as a positional system. We use a positional system today and it means that the position of a symbol tells you about its value. This makes numbers easier to write and use to record large numbers as well as potentially making calculations easier. The written version of the numbers was called cuneiform:
They still used bases 10 and 60, but the positions of the symbols also had information about their value. So, what the Babylonians saw was based on numbers up to 60 formed by the tens and the ones symbols:
![]()
These groups of symbols were then positioned according to whether they were ones, sixties and so on... For example
|
60 x 60
|
60
|
Ones
|
||||
|
3600
|
60
|
1
|
||||
|
Image
|
Image
|
Image
|
||||
|
2 x 3600
|
7 x 60
|
39 x 1
|
||||
|
7200
|
+
|
420
|
+
|
39
|
=
|
7659
|
Try this one (answer at the end):
![]()
Remember, the groups of symbols represent (from right to left) ones, 60's, 3600's, and so on, rather than the ones, 10's, 100's we use today, but very clever all the same!
The "Not so Clever" Romans
We use the numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and using these numerals we can write any number. The position of the digit tells us its value - so a 1 at the right means one unit but depending on where it is placed it can be worth 10 or 100 or 1000 and so on. Of course this makes the zero very important. Can you think why?The Romans only had a limited number of symbols I, V, X, C, L, D, M and from these they generated their numbers using what was very like a tally system with some shortcuts:
The numbers 1 to 10 (no zero notice) are:
I, II,III, IV,V, VI, VIII, IX, X
Then other numbers were created by using a combination of I's, V's and X's and the letters L (representing 50), C (standing for 100), D (500), M (1000).
So, for example 111 = CXI - could you have guessed that?
Notice the way 4 and 6 are written 4 is one less than 5 so it is written with the symbol for 5 (V) with a 1 (I) in front of it telling you that 4 is one before the 5. Because 6 is one more than 5, the I is put after (6 is one after 5). In the same way 9 is one before 10. So you could write 90 as XC (10 before 100).
Here are some more:
20 XX
25 XXV
29 XXIX
75 LXXV
2007 MMVII
1999 MCMXCIX (1000 + 100 before 1000 + 10 before 100 + 1 before10).
Now try these:
XXXVI
XLVII
DCCLVI
MCMLXIX
The Romans could only count
For the Romans large numbers were a pain, as you can see, but their number system was also useless when it comes to doing any calculations. Try this and see if you can do it without rewriting the problem using our number system:
They had two problems - firstly they did not have zero and secondly they did not have a system which allowed for "place value" in other words the position of a number told you nothing about its value (so in Roman numerals a C means 100 wherever you see it). Whereas, in our number system you know the value of a number by its column counted from the right (ones, tens, hundreds, etc.)
The Romans, and Greeks, did not have a zero and their ability to calculate suffered as a result.
The Magic of Zero
It was not until 2400 years ago that zero appeared in any number system and the Babylonians were first! They were followed by the Mayans. But, it was not until 2300 years ago that the beginnings of our modern number system, which depends on place value and needs a symbol for zero, appeared in India and its surrounding regions.It was the trading of the Arabs that helped to spread the Indian system widely to Western Europe.
A useful number system took about 12000 years to arrive!
So what is zero for?
Zero really has two main purposes in our number system:Firstly, it represents nothing - it enables us to write in symbols the fact that nothing is left, or there to start with.
Secondly it enables us to make an empty space in a number. For example in the number 650,081 the zeros tell us there are no hundreds and no thousands. Without the zeros our place value system would not work as we would not be able to distinguish 650,081 from 6,581.
But we also use zero to mean other things. Often we use it to create a reference point. For example:
When we talk about the height of land we mean its height above sea level. This means that someone decided that sea level would be at zero height.
The freezing point of water is zero when measuring temperature in centigrade but not in Fahrenheit. The freezing point of water is 32 degrees Fahrenheit. Zero Fahrenheit was the coldest temperature that the German-born scientist Gabriel Daniel Fahrenheit (after whom the scale is named) could reach with a mixture of ice and salt.
"Absolute zero" is -273.15 degrees centigrade. Absolute zero relates to the oscillation of molecules or atoms. In all materials a point is eventually reached at which all oscillations are the slowest they can be. This point is called 'Absolute zero'. You can never reach absolute zero.
'Nothing is real'
The Beatles
....or perhaps not!
Answers:
King Narmer's Club:
400,000 bulls; 1,422,000 goats;120,000 human prisoners
Babylonian cuneiform:
![]()
36 x 3600 + 40 x 60 + 11 = 132,011
Now try these:
36, 47, 756, 1969
We can only count:
MMMDCCCI
