What's in the Box?

Four numbers in little boxes are put into a special big box that does a multiplication, then four new numbers come out at the end:


We only used whole numbers to go in, so, what multiplication might have gone on in the big box to get the answers in the picture above?

What was the largest number that could have been used to multiply by, in that big box?

Imagine four new boxes now (with new numbers in) and the large box multiplying by a different number this time. The numbers that come out are these:


What would be the number that the big box is multiplying by?
How are you working these out?
Discuss with others and see if there are different ways that you found the answers.

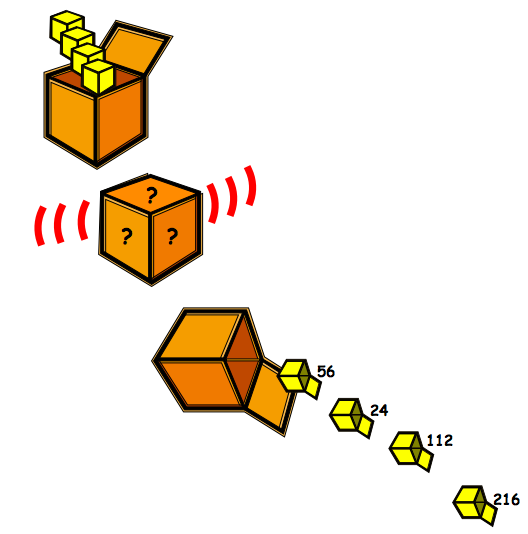
Why do this problem?

Of course this problem is rather like a function machine, but it can be more interesting for the pupils and easily extended to challenge a wide range of pupils. It could be used to introduce children to the idea of common factors and offers opportunities for learners to record in whatever way they choose.

Possible approach

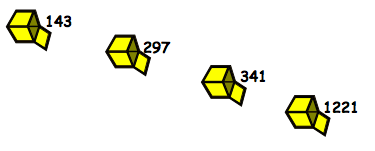
It may be necessary to introduce the class to just one number going in and to give them one outcome to start with so that they understand the process. Then, gradually increase the number of numbers going in until you reach four, as in the problem. Your own examples can be adjusted in complexity according to the level of your pupils.

Once learners have had some time to work on the first part of the problem in pairs, ask them to share their ways of working with the whole group. Look out for those who give good reasons for choosing particular methods. At this stage, you could introduce the vocabulary of common factors if appropriate.

You may also wish to draw attention to interesting ways of recording.  Some children may have drawn pictures, others may have written calculations and others may have done both.

Key questions

Possible extension

Pupils can be challenged to explain how they know they've found the largest possible number that the inputs have been multiplied by. Some pupils could go on to invent their own similar problems for others to do, including ones where a division is performed inside the box instead of a multiplication.

Possible support

Some pupils might benefit from beginning with the version of this task that uses addition and subtraction: What Was in the Box?

In order to introduce the multiplication version of this task, you can use sticks of cubes (such as multilink cubes) to represent one number going into the 'box'. Cover the cubes with a cloth and then secretly add the required extra number of cubes under the cover, in the form of more sticks of cubes, before revealing them to the child. Then a number of probing questions can be asked: How many cubes are there now? What has happened under the cover? Encourage pupils to consider how the number of sticks has grown, e.g. from 1 to 5, instead of simply counting how many more cubes there are.

As they tackle the main problem, some learners might find it useful to have a multiplication square or calculator available.