Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Peg Rotation
Age 7 to 11
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Peg Rotation
Here we have a kind of peg board. The holes go all the way through so the pegs may be seen from the top or underneath.
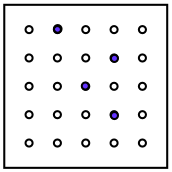
You'll see the 4 blue pegs.
Now the peg board is either:
- flipped over - north to south, OR east to west, OR north-east to south-west, OR north-west to south-east;
- or it is rotated clockwise or anticlockwise.
Can you find out which movements could produce the four next views?
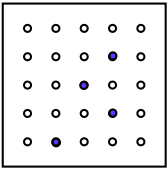
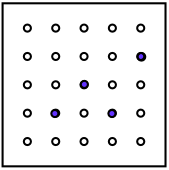
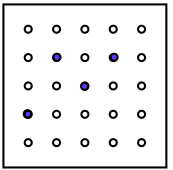
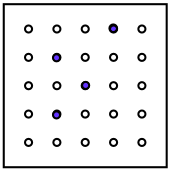
You could make some of your own and get your friends to see if they can find how you've moved it to make your next picture.
Try now to put 4 pegs in so that when you do a move with the board it still looks the same.
Now I've made a triangular board to do the same things.
Here's the starting view:

How has it been moved to show these views?
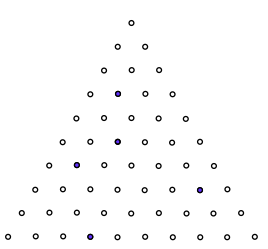

Hope you've had fun exploring these.
Can you think up ways of changing what I've done so that you can explore further?
Why do this problem?
This challenging activity offers a context in which learners can apply knowledge of transformations. Although best done practically for many pupils, some may draw on visualisation skills, at least to make hypotheses before confirming practically. The triangular arrangement of dots helps to familiarise pupils with different angles.Possible approach
This activity, as well as being done in ones or twos by the pupils, could be introduced by you challenging all the class at once. The first picture could be presented on screen, and you could ask the pupils what they would have to do with it to to see the next two pictures. You could provide pairs or small groups of pupils with an acetate grid and some dry-wipe pens to create each image for testing.You may wish to download and print these sheets for pupils:
PegRotation.pdf
PegRotation2.pdf
(The first contains just the square grids, the second contains the triangular grids.)
Key questions
Which peg/s might be helpful to focus on to begin with?Have you tried flipping/rotating the original grid?
Possible extension
As suggested in the question itself, learners could be challenged to tweak the task slightly and pose their own problems. For example, they could use more/fewer blue pegs; use a different grid etc. Also go to "Taking a Dice for a walk"Possible support
Plenty of dotty paper will be helpful and/or dotty grids on acetate sheets so that pupils can compare two patterns easily.You may also like
Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?