Copyright © University of Cambridge. All rights reserved.
'Magic Matrix' printed from https://nrich.maths.org/
Show menu
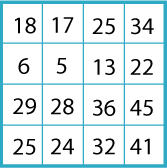
Here is a "magic" matrix:
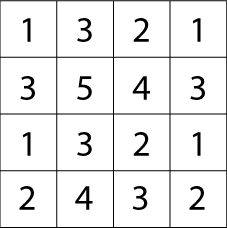
It doesn't look very magical does it?
This is how you find out the "magic" in the matrix:
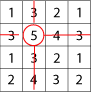
Circle any number in the matrix, for example, $5$. Draw a line through all the squares that lie in the same row and column as your selected number:
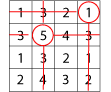
Repeat for a third time, for example:
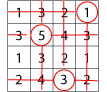
Then circle only the remaining number that has no line through it:
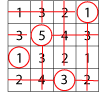
Add all the circled numbers together and note your answer.
Try again with a different starting number. What do you notice?
Try the same thing with these two slightly harder matrices:
This problem was made to celebrate NRICH's tenth birthday - perhaps you can see the connection!
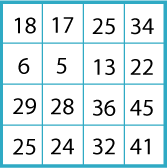
Let's try a different one with larger numbers.
Now make an addition table like this:
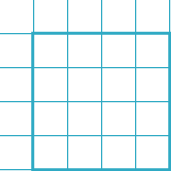
You can download a sheet of them here.
Put your numbers in the cells on the outside and add them to make the matrix:
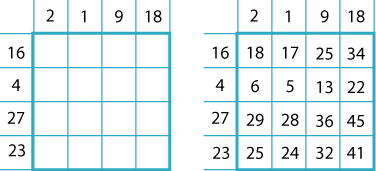
Finally, copy the square without the numbered outside cells:
Now you know how the matrix works, you are ready for the real problem.
Can you work out what numbers were used to make any of the original three matrices?

It doesn't look very magical does it?
This is how you find out the "magic" in the matrix:
Circle any number in the matrix, for example, $5$. Draw a line through all the squares that lie in the same row and column as your selected number:

Then circle another number that has not got a line through it, for example, the $1$ in the top right hand corner, and again cross out all squares in the same row and column:

Repeat for a third time, for example:

Then circle only the remaining number that has no line through it:

Add all the circled numbers together and note your answer.
Try again with a different starting number. What do you notice?
Try the same thing with these two slightly harder matrices:
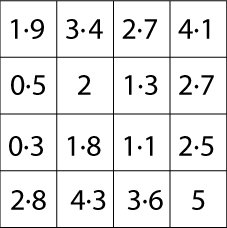 |
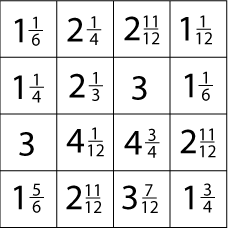 |
This problem was made to celebrate NRICH's tenth birthday - perhaps you can see the connection!
Let's try a different one with larger numbers.

What is the magic total this time?
I will show you how this kind of matrix works. You can then invent one to try on your friends!
First you need to choose your 'magic total'. As you know, I chose $100$ for the matrix above.
I have chosen: $1, 16, 9, 23, 18, 4, 2$ and $27$. [You can check that together they add to $100$.]
Now make an addition table like this:

You can download a sheet of them here.
Put your numbers in the cells on the outside and add them to make the matrix:

Finally, copy the square without the numbered outside cells:

Now you know how the matrix works, you are ready for the real problem.
Can you work out what numbers were used to make any of the original three matrices?