One to fifteen
Problem
Can you put the numbers from 1 to 15 on the circles so that no consecutive numbers lie anywhere along a continuous straight line?
Getting Started
Which circles lie on the fewest straight lines? How might this help?
If you try putting the number $1$ on one circle, where could you put the $2$? Now, where could the $3$ go?
You could use the interactivity to try out your ideas.
You could print off this picture of the circles and use numbered counters to solve the problem, or use a pencil to write numbers in the circles.
Student Solutions
Thank you for all your solutions to this problem. Many of you sent in a way of completing the challenge - unfortunately there are too many to name you all. Lu-Lu, James and Sam from St Nicolas C of E Junior School, Newbury commented:
We found lots of different solutions. We noticed that 1 and 15 had less consecutive numbers than the other numbers. 1 has only 2 and 15 has only 14. The other numbers, 2, 3, 4, ......,12 and 13 have two consecutive numbers each. So it's best to put 1 and 15 in the middle, but we did find other solutions as well.What a sensible way to start the problem - well done to you three! Many pupils from Eastwood Primary School sent us solutions. Rajal explained:
We looked at all the numbers then we started with 11, 15 and 13. Then we did the numbers 14, 1, 6, 10 and 3. Then we made sure that no consecutive numbers were there. This allowed us to put most of the numbers in place but a few of the last ones caused problems. We played around with these until they all were correct.This is another good way to approach the problem - using a bit of trial and improvement. Here is Rajal's solution:
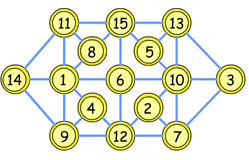
Luke and Daniel from Whingate Primary in Leeds sent a slightly different solution:
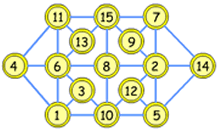
As Lu-Lu, James and Sam say, there are many different ways to complete this problem - perhaps you have found one which is not the same as these two - but thank you to those of you who gave help with good ways of going about it. That's what NRICH is looking for!
Teachers' Resources
One to Fifteen
Can you put the numbers from 1 to 15 on the circles so that no consecutive numbers lie anywhere along a continuous straight line?
Why do this problem?
Possible approach
Key questions
Possible extension
Learners could be challenged to find as many different solutions they can.
Possible support
Using numbered counters and the challenge sheet will help all learners access this task. Encourage the use of 'trial and improvement', emphasising that this task is not about about finding an answer quickly.