Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
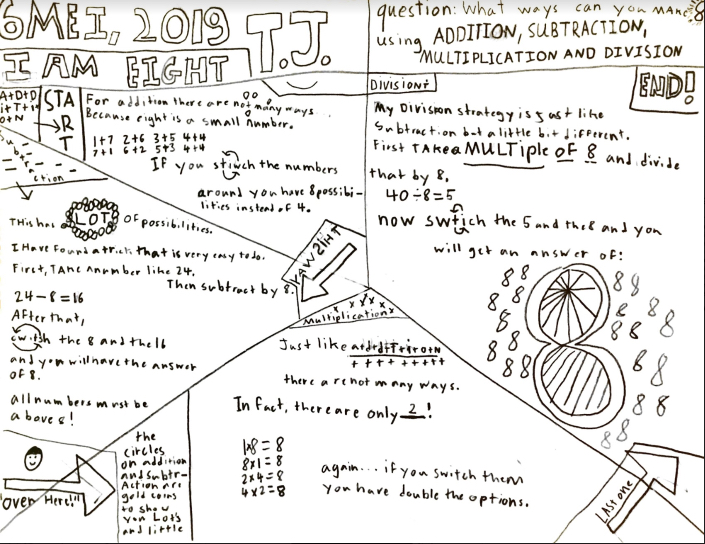
I'm Eight



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
We had over 70 solutions sent in for this task!
Tayla from Marion Primary School in Australia and Luna from Marner Primary School in England, sent in what they called “all the possible additions equalling 8”:
5+3 =8 3+5 =8 6+2=8 2+6=8 1+7=8 7+1=8 4+4=8
and then the subtractions:
9-1=8 10-2=8 11-3=8 12-4=8 13-5=8 14-6=8
PomPom from the Australian International School Malaysia extended the idea and used a division making 12:
6+6=12, -20+32= 12, 24$\div$2= 12
Micaela from the Westridge School for Girls went further by using more than two numbers to generate the solution:
For the number 8 I did 100 minus 48 minus 32 minus 4 minus 8 which equaled eight.
Now for a random age of 10 I did 87 minus 16 minus 11 then subtract 50. That's both of my answers.
Adelaide and Janeen also from Westridge used all four operations:
0+8=8 Eight minus eight equals zero, so eight plus zero must equal eight.
19-11=8 Eleven plus eight equals nineteen, so nineteen minus eleven must equal eight.
2x4=8 Eight divided by two equals four, so two times four must equal eight.
24$\div$3=8 Eight times three equals twenty-four, so twenty-four divided by three must equal eight.
2+6=8 If eight minus six equals two, then six plus two must equal eight.
99-91=8 Eight plus ninety-one equals ninety-nine, so ninety-nine minus ninety-one must equal eight.
1x8=8 Any number times one equals itself.
64$\div$8=8 Eight times eight equals sixty-four, so sixty-four divided by eight must equal eight.
3+5=8 Eight minus five equals three, so three plus five must equal three.
55-47=8 Eight plus forty-seven equals fifty-five, so fifty-five minus forty-seven must equal eight.
All the ways to make eight is infinite but these are just a few examples.
Sofia and Alicia also from Westridge produced fifty altogether but went further by using different operations in one calculation (click on the image to see it larger):

Noah, Oania, Jasmine, Nabil, Rayyan, Luna, Nibir, Rheshai, Arafat, Yasmiin, Sheum, Aadam, Haifa, Mahira, Faridah, Yunus, Ismat, Chloe, Maryam, Nabeeha, Qiyyama, Oania and Yusuf from Marner Primary School London sent in their solution, which also mentions how they knew those solutions:
96 divided by 12 equals eight. You can use inverse to check your answer as 12 x 8 = 96
100-92=8 I know this because 92+8=100
3x3-1=8 3x3 is 9 and -1 is 8.
A way to make 8 is when you have the number 100 and take away 92 because 100 -90=10 and 10-2=8!
2+6=8; 3+5=8; 4+4=8; 5+3=8: 6+2=8: 7+1=8; 4+4=8; 64 divided or shared by 8=8; 2+2+2+2=8
16÷2=8 I know this because there are 8 2's in 16.
A way is 96 divided by 12=8 that is the answer; 8+33-33=8
I know that you can make 8 by timesing 2 and 4 and that also will make 8; 7+1=8 I know this because 1+7=8; 100-92=8 I know this because 100-2=98 and when taking away, the first 2 numbers, you can switch those numbers around.
80 take away 72 equals 8; 5 add 3 equals 8 16 divide it by 2 equals 8 18 take away 10 equals 8; 4 add 2 add 2 equal 8 14 take away 6 equals 8; 1+7=8 8+0=8 5+3=8 3+5=8 0+8=8 double 4=8 2x4=8 11-3=8 7+1=8; 16 divided by 2=8
80÷10=8 because I counted in my head and it worked.
100-92=8 I know this because 8+92=100.
We had twenty three very different solutions in from the International School in Brussels. Some kept to the idea of making 8, others used their own ages as the target number. Click on any of them to download all twenty three in a Word Document. It's worth looking at them for the mathematics and the display styles. Thank you to Alessandro, Amo, Andrey, Arthur, Ben, Eleanor, Elise, Emma, Evie, Fede, Gonzalo, Heleen, Jack, Javier, Luna, Marina, Niko, Quinn, Raila, Suzy, TJ and Zoe.
| Here is Luna's, offering an original display and a variety of solutions: |
Here is Eleanor's, using ideas that are very different from others: |
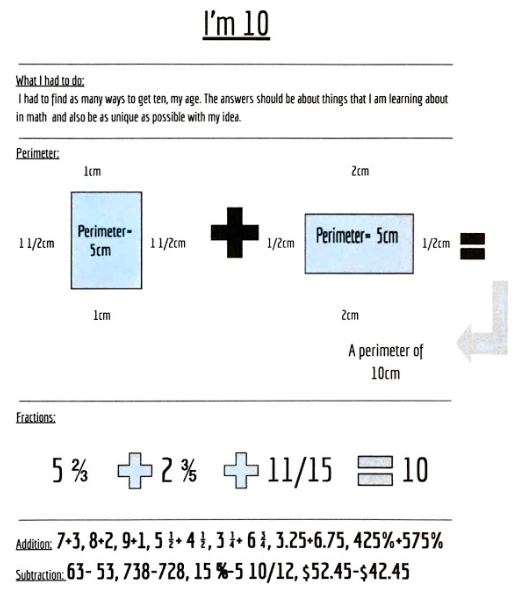
| Here is Evie's who separates ideas well. I like the idea of adding in "bonus" ones. It looks as Evie has enjoyed herself here! |
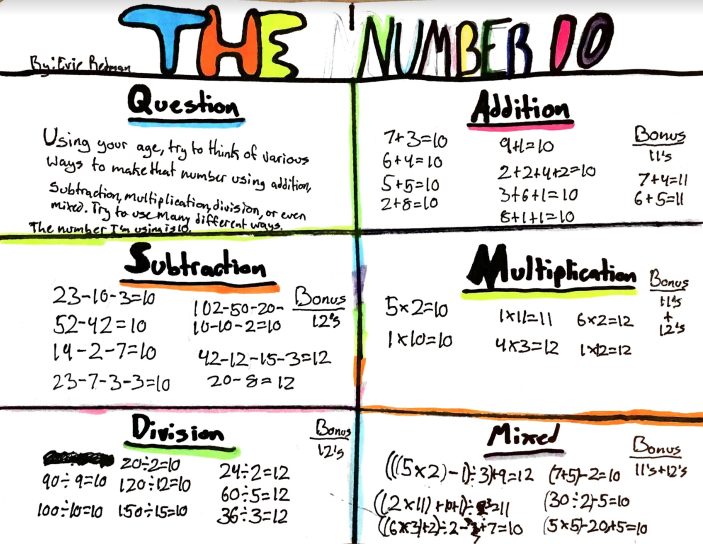
Here is TJ's. As well as an interesting display there's a lot of reversing going on. I think it's good to explore in this way! |
What a great response, so many thoughtful ideas for both the maths and the way of communicating it. Thank you all very much.