Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.
    

    


Robert from Kings Ely said this very concisely:

The vector for the flags is $\frac{n-1}{n}$ of the vector of centres.

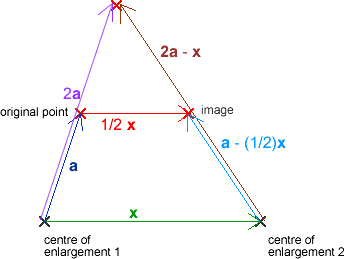
See if you can follow this explanation of why this is the result using this diagram:

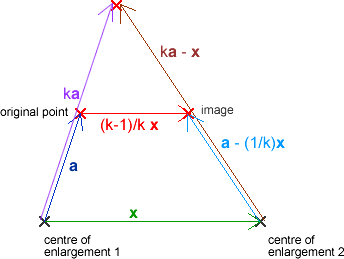
Suppose the first scale factor is $k$ (so the second one is $\frac{1}{k}$). Let $\mathbf{x}$ denote the vector from the first centre of enlargement to the second. Then the required transformation is a translation by the vector $\frac{k-1}{k}\mathbf{x}$.

To see this, consider a single point on the flag. (If we show that the required transformation for a single point is the given translation, then the same will apply to the flag.) Let $\mathbf{a}$ denote the vector from the first centre of enlargement to the point. Then the vector from the first centre of enlargement to the image of the point under the first enlargement will be $k\mathbf{a}$. The vector from the second centre of enlargement to this image will be $k\mathbf{a}- \mathbf{x}$, so the vector from the second centre of enlargement to the final image will be $\frac{1}{k}\left(k\mathbf{a}-\mathbf{x}\right) =\mathbf{a}-\frac{1}{k}\mathbf{x}$. So the vector from the initial point to the final image will be $-\mathbf{a}+\mathbf{x}+\mathbf{a}- \frac{1}{k}\mathbf{x}=\frac{k-1}{k}\mathbf{x}$, as required.