Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Who is the fairest of them all ?
Age 11 to 14
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Isabel from St Andrew's Scots School in Argentina used Geogebra to investigate the problem. This is Isabel's work, with some teacher comments.
Robert from Kings Ely said this very concisely:
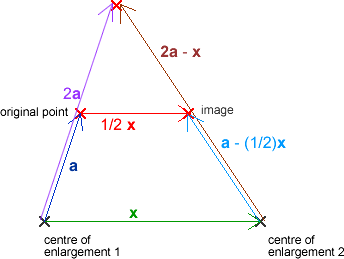
See if you can follow this explanation of why this is the result using this diagram:
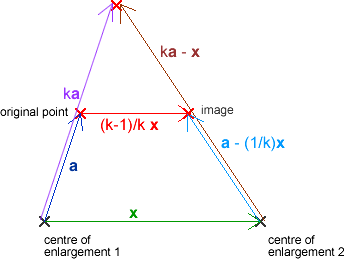
Suppose the first scale factor is $k$ (so the second one is $\frac{1}{k}$). Let $\mathbf{x}$ denote the vector from the first centre of enlargement to the second. Then the required transformation is a translation by the vector $\frac{k-1}{k}\mathbf{x}$.
To see this, consider a single point on the flag. (If we show that the required transformation for a single point is the given translation, then the same will apply to the flag.) Let $\mathbf{a}$ denote the vector from the first centre of enlargement to the point. Then the vector from the first centre of enlargement to the image of the point under the first enlargement will be $k\mathbf{a}$. The vector from the second centre of enlargement to this image will be $k\mathbf{a}- \mathbf{x}$, so the vector from the second centre of enlargement to the final image will be $\frac{1}{k}\left(k\mathbf{a}-\mathbf{x}\right) =\mathbf{a}-\frac{1}{k}\mathbf{x}$. So the vector from the initial point to the final image will be $-\mathbf{a}+\mathbf{x}+\mathbf{a}- \frac{1}{k}\mathbf{x}=\frac{k-1}{k}\mathbf{x}$, as required.
Here is the diagram with k=2: