Copyright © University of Cambridge. All rights reserved.
'Maths Trails' printed from https://nrich.maths.org/
Show menu
The NRICH team are always looking for new ways to engage teachers and pupils in problem solving. Here they explain the thinking behind their latest creation - maths trails. You can find out how to obtain the trails here.
What do we see as the purposes of teaching mathematics? What exactly are we trying to encourage in our mathematics classrooms? These are "big" questions which we are not going attempt to answer fully in this article, but we would like to suggest that one aim is to give pupils the experience of feeling like a mathematician and therefore being mathematical. Being mathematical has many different interpretations, but some descriptions of what it means might include:
- thinking about and communicating ideas;
- engaging in problem-solving activities;
- creating and identifying mathematical problems within given contexts.
It is clear that some knowledge of mathematics is involved in
the above. Whilst the regurgitation of facts or the use of a
certain skill in a particular context (for example, being able to
do long multiplication) are useful, they are only valuable when
they help us to solve problems. So, if much of mathematics is not
about learning facts and practising skills, how can we support
learners in being mathematical? They need opportunities to explore
problems and to pose problems of their own. We need to guide and
structure our pupils' experiences if we are to support problem
solving effectively. This is where we hope the NRICH Maths Trails
come in. The purpose of the Trails is to be more explicit about the
skills learners need to develop in order to become better problem
solvers.
Problem solving and mathematical thinking
What is problem solving?
When we are presented with a mathematical problem, it is only
a problem if we do not immediately know how to solve it. The
process of problem solving is like a journey from a state of not
knowing what to do, towards a destination which we hope will be the
solution. The key is to have some strategies at our fingertips
which will help us to identify a possible route through to a
solution. Our mathematical journey is often full of twists and
turns where we revisit ideas or need to step back and look for
alternatives. Often a mistake or dead-end gives vital clues to the
mathematics of the problem and is therefore crucial in the solution
process.
Polya (1945) was certain that teachers can help pupils to
become better problem solvers by making the methods of problem
solving transparent. The framework he devised for problem solving
consisted of 'four phases': understanding the problem, devising a
plan, carrying out the plan and looking back. Other authors have
slightly different takes on the stages occurring in the
problem-solving process. Mason et al. (1982) define three steps
which they call 'Entry, Attack and Review'. Burton (1984)
supplements these with a fourth which she labels 'Extension'.
Piggott (2004) also proposes four 'elements' in what she terms the
CAPE model: 'Comprehension, Analysis and synthesis, Planning and
execution, and Evaluation', which are outlined in more detail in
the Trails books. These frameworks give us a general feel for the
processes we go through when solving problems, but on their own
they lack sufficient detail. They are useful in order to identify
where we are in the problem-solving process but what particular
strategies will help us begin to understand the problem or
interpret our findings?
What is mathematical thinking?
The particular mathematical skills we need to use when problem
solving are more than numeric, geometric and algebraic
manipulation. They include ideas such as:
- modelling;
- visualising;
- being systematic;
- generalising.
We would class these skills as elements of mathematical
thinking that are needed to engage in mathematical problem solving.
To date, we have published two Trails books, one focusing on
generalising and the other on working systematically.
A Trail can be used as a "course" for pupils over a short or
long period of time, working as a whole class, or in small groups
or individually. Each Trail indicates an ordering of the materials
to support each pupil's developing skills over time. However, it is
also possible to dip in and out of the materials. The ordering of
problems is not intended to be a straitjacket. The problems offer
opportunities for pupils of a wide age and ability range, and do
not imply a particular view of classroom organisation. However,
there is an underlying message concerning classroom practice and
the learning of mathematics as a collaborative experience, valuing
the journey through a problem rather than the answer. While there
is no need to offer group-work opportunities there is an
underpinning expectation that pupils will be given opportunities to
talk about their mathematical experiences en-route as well as at
the "conclusion" of their studies. Models of using a Trail with the
whole class, small groups or individual pupils are described in the
books.
And here's a taste...
So, let's look at a couple of examples from the Trails. The
Generalising Trail begins with a section on generalising from
patterns and the first problem is Colour Wheels .
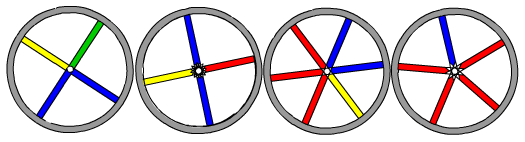
In the notes for teachers in the book, we suggest the value of
this activity as a demonstration of the power of using mathematical
knowledge to predict and explain patterns. This power is perhaps
more apparent in Colour Wheels than in other problems as the visual
context means that it is not immediately obvious as mathematical.
Ideas for how to introduce this activity are outlined in the book.
This might involve modelling the creation of colours by using a
circular disc with colours marked on its circumference. Pupils
could be asked to close their eyes and imagine a wheel which
produces a similar pattern and then describe or draw on whiteboards
what they see. After considering the first sequence as a whole
group, we have suggested encouraging pupils to work in pairs or
small groups on the rest of the problem. In the notes, we offer
guidance in the form of questions and prompts which will help
students to:
- build up ideas by describing what they see;
- model the wheel either physically or numerically;
- look for patterns and note where the repeats occur;
- build upon their notion of multiples and divisibility.
For each problem in the trail, we have also recommended ideas
for a plenary. In the case of Colour Wheels this could be an
opportunity to discuss methods and findings from different groups
regarding divisibility and remainders. In addition, we suggest that
there is a chance here to comment on a method you might have chosen
as a "teacher problem solver".
Pupils are often asked to "go away and be systematic", but we
are often not clear about what this means. We cannot assume that
someone can go away and, as if by magic, begin acting more
systematically. There are skills we can identify that are about
working systematically which can be discussed and shared with our
pupils and the Working Systematically Trail aims to support this
dialogue. In this Trail we identify three main strands, or ways, in
which you can work systematically:
- Interpretation: where data or information within a problem accessed in a systematic way enables entry into the solution.
- Framing: taking meaning from playing with the problem -recording outcomes which lead to identifying patterns that need to be validated. In this case, the system adopted helps identify a property which needs explaining.
- Deduction: part of the explanation and underlying mathematics comes from the ability to plan and organise inputs to one or more algorithms.
Of course some problems can be solved using a mixture of the
above. We feel that it is important to highlight the different
features of working systematically to pupils so that they can begin
to identify for themselves the sorts of strategies they are
employing, or could employ, when solving problems.
The starting point of the Working Systematically Trail is
A Mixed-up Clock .
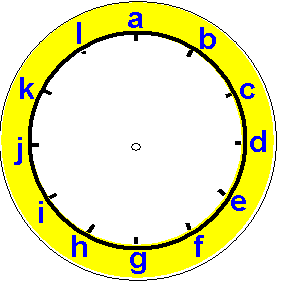
In the teachers' notes, we highlight that the solution to this
problem can only be approached by systematically interpreting
information given in the clues and so this of course fits into the
category of Interpretation identified above. We suggest that a
"warm up" which serves to remind pupils of the meanings of number
properties (such as odd, even and consecutive) might be a good way
in to this problem. Students could be invited to:
- suggest two numbers whose product is an odd number less than 100;
- find out how many different sets of three consecutive odd numbersthere are between 50 and 70;
- find the largest and smallest totals they can make using three consecutive odd numbers between 50 and 70.
We then go on to offer guidance on introducing the problem as
it stands to the children. Initially looking at clues altogether,
but revealing them one by one, provides a good opportunity to talk
about which clues are immediately helpful and which must be put
aside at first. This encourages the pupils to prioritise the
information and to realise that it may not always be appropriate to
start at the beginning and work downwards! We suggest that in a
plenary it would be interesting to discuss the point at which there
is an element of choice in the order the clues are utilised.
In conclusion
All the questions in the Trails books can be used in an
appropriate curriculum content context rather than taught in
isolation, but the important thing is that there is a journey to
make and problem-solving skills with which we need to become
familiar. We hope that, after tackling some of these problems,
learners will recognise appropriate opportunities to generalise or
work systematically and talk about generalising or working
systematically when those occasions arise in the future.
The books will not necessarily make those who use them expert
problem solvers, but we hope that they will help unravel some of
the mysteries we encounter on problem-solving journeys.
You can find out how to obtain the trails
here.
Bibliography
Burton, L. (1984) Thinking
Things Through . Oxford: Basil Blackwell Limited.
Mason, J. with Burton, L. and Stacey, K. (1982) Thinking Mathematically . Wokingham:
Addison-Wesley Publishing Company.
Piggott, J. (2004) Mathematics enrichment: what is it and who is
it for? Paper presented at the British Educational Research
Association Annual Conference, University of Manchester, 16-18
September 2004.
Polya, G. (1945) How to
Solve It . London: Penguin Books Limited.
This article also appears in Primary Mathematics, a journal published by The Mathematical Association .