Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Tuning and Ratio
Age 16 to 18
Challenge Level 





You don't have to know any music theory to do this question as all you need to know is explained here. You only need to know about logarithms. The actual problems to solve are given in bold italic text.
Diagram showing part of a piano keyboard.
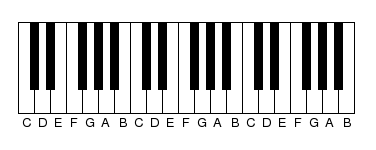
Wherever you are on the keyboard, the interval between one note and the next with the same letter name is always an octave. In the same way, the interval between C and the G above it, or D and the A above it, or anything similar (seven steps on the keyboard, including both black and white notes), is always a fifth. Each of these intervals, the octave, the fifth, and
others, corresponds to a particular ratio of string lengths which produce the notes. The octave corresponds to 2/1, halving the length of the string. The fifth corresponds to 3/2, taking two thirds of the length of the string. The interval from C to F, called a fourth, has the ratio 4/3.'Fourth' and 'fifth' etc. are musical terms and do not refer to the fractions 1/4 and 1/5.
The interval from F to G, between the fourth and the fifth, has the ratio ${3/2 \over 4/3} = 9/8$. This interval is called a tone and it is also the the interval from C to D. Notes tuned in these ratios produce pleasant harmonies but compromises have to be made in tuning the other notes because the ratios do not relate to each other exactly. This problem is about
discovering what the compromises might be. The table below shows some musical intervals and the corresponding ratios of the notes with respect to the note C.
| C | D | E | F | G | A | B | C |
|
1/1
unison
|
9/8
tone
|
81/64 |
4/3
fourth
|
3/2
fifth
|
27/16 | 243/128 |
2/1
octave
|
You might expect there to be three tones in the interval from C to F, changing the ratio by 9/8 then 9/8 again and then 9/8 a third time, that is ${(9/8)}^3$. How does this compare with the ratio 4/3?
Pythagorean tuning kept the ideal ratios for the octaves, fifths and fourths and tuned the note E with a ratio ${(9/8)}^2$ and the notes A and B with the ratios $(3/2)\times (9/8)$ and $(3/2)\times {(9/8)}^2$. This system preserves the ratios of the fourth and fifth but produces a major third, from C to E and a major sixth, from C to A, which sound unpleasant. The Greeks were not interested in these intervals, but when composers in the middle ages and Renaissance wanted to use them, a new system of tuning was needed.
Just intonation (shown in the table below) has much better major thirds and major sixths, of 5/4 and 5/3. It tunes the B so that the interval from E to B is a perfect fifth and the interval from G to B is a perfect third. But it does this by having two different sizes of tone: the intervals C-D and D-E are different here, but they were the same in the Pythagorean scale. Find the ratio corresponding to B. Also compare the D-A ratio with the ideal fifth (3/2).
| C | D | E | F | G | A | B | C |
|
1/1
unison
|
9/8
tone
|
5/4
third
|
4/3
fourth
|
3/2
fifth
|
5/3
sixth
|
? |
2/1
octave
|
Just Intonation
You might expect there to be six tones and twelve semitones in an octave (because there are 12 notes) but again that is not exactly so. Find exactly how many tones there are in an octave by finding what power of $9\over 8$ gives 2. Find also exactly how many major thirds there are in an octave.
In the equal tempered scale, the standard tuning nowadays, these mismatches between different ratios are removed by defining the intervals differently. The tone is made a little smaller, so that there are exactly six of them in an octave. The semitone (half a tone) is a twelfth of an octave: so its ratio is ${(2)}^{1/12}$. If, for example, the note C is tuned with a string length of 32 units then the C# is tuned with a string of length ${32\over {(2)}^{1/12}}=30.2$ (to 3 significant figures). This applet by Benjamin Wardhaugh demonstrates the relationship between the string lengths and the notes. The ratio ${(2)}^{1/12}$ is used to build up the other intervals, so that each interval is a whole number of semitones, and the ratio between its frequency and the frequency of the lowest note in the scale is given by a power of ${(2)}^{1/12}$. For example the fifth is ${(2)}^{7/12}$.
Instrument tuners customarily use a logarithmic unit of measure, the cent, where 1200 cents are equal to one octave, a frequency ratio of 2/1, so that a cent is a 1200th root of 2. The table below shows the Equal tempered, Pythagorean and Just systems of tuning given in cents showing how many cents the note lies above the starting C. Fill in the table.
| C | D | E | F | G | A | B | C | |
| Equal tempered scale | 0 | 200 | 400 | 500 | 700 | 900 | 1100 | 1200 |
| Pythagorean scale | 0 | 702 | 1200 | |||||
| Just intonation | 0 | 386 |
702
|
1200 |
[See also the article Euclid's Algorithm and Music]