Pick's Theorem states that if a polygon has vertices with integer coordinates (lattice points) then the area of the polygon is $i + {1\over 2}p - 1$ where $i$ is the number of lattice points inside the polygon and $p$ is the number of lattice points on the perimeter of the polygon.

Define Pick's function for a polygon $P$ as $$F(P)= {\rm area }(P) - \left(i + {1\over 2}p - 1\right)$$ where $i$ and $p$ are defined as above. To prove Pick's Theorem, we have to show that this function takes the value zero for all planar polygons. You will need to use the fact that any polygon can be split into a finite number of non-overlapping triangles.

The sequence of five steps in this proof starts with 'adding' polygons by glueing two polygons along an edge and showing that if the theorem is true for two polygons then it is true for their 'sum' and 'difference'.
The next step is to prove the theorem for a rectangle, then for the triangles formed when a rectangle is cut in half by a diagonal, then for the general triangle (labelled $T$ in the diagram below), and finally for any planar polygon because it can be built up from 'adding' triangles. Although the proof is long it is simply a matter of counting points.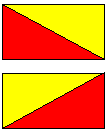

(1) Let $P_1$ and $P_2$ be non-overlapping polygons that abut along a common edge $AB$. Let $P$ be the union of $P_1$ and $P_2$ and $i, i_1$ and $i_2$ the lattice points inside and $p, p_1$ and $p_2$ the lattice points on the perimeter of $P, P_1$ and $P_2$ respectively. Prove that if Pick's function is zero for any two of these polygons it must be zero for the third.

(2) Prove that Pick's function is zero for the rectangle with vertices $(0,0), (a,0), (0,b)$ and $(a,b)$ where $a$ and $b$ are integers.

(3) Two triangles are produced when the rectangle with vertices $(0,0), (a,0), (0,b)$ and $(a,b)$ is cut in half by one or other of the diagonals. Prove that Pick's function is zero for these triangles and hence that Pick's Theorem holds for any right-angled triangle with sides parallel to the axes.

(4) Prove that Pick's Theorem holds for the general triangle $T$ shown in this diagram. (5) Prove that Pick's Theorem holds for any planar polygon.