Copyright © University of Cambridge. All rights reserved.
'Spiroflowers' printed from https://nrich.maths.org/
Show menu
A spirolateral is a continuous path drawn by repeating a sequence of line segments of lengths $a_1, a_2, a_3, ... a_n$ with a given angle of turn between each line segment and the next one. (Alternatively the path can be considered as a repeated sequence of 'bound' vectors: $\overrightarrow {P_1P}_2, \overrightarrow{P_2P}_3,... \overrightarrow{P_n P}_{n+1}$, each vector starting at the endpoint of the previous vector.)
 |
 |
 |
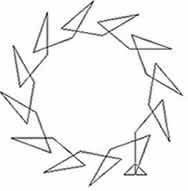
In the first diagram the lengths of the line segments are
equal and the angles of turn vary periodically in sequences of
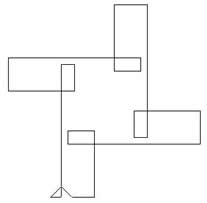
length 3. In the second diagram the lengths of the line segments
vary periodically in sequences of length 5 and the angles of turn
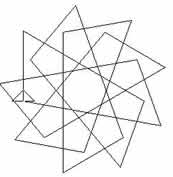
are equal. In the third diagram both the lengths and the angles
vary.
Investigate these patterns, give sequences of instructions
which would produce similar paths and explain why in each case the
spirolateral paths are closed producing a cyclic pattern when the
sequence is repeated infinitely often.
| Why does the spirolateral in this diagram continue indefinitely, shooting off to infinity if the sequence is repeated infinitely often? |