Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Spiroflowers
Age 16 to 18
Challenge Level 





A spirolateral is a continuous path drawn by repeating a sequence of line segments of lengths $a_1, a_2, a_3, ... a_n$ with a given angle of turn between each line segment and the next one. (Alternatively the path can be considered as a repeated sequence of 'bound' vectors: $\overrightarrow {P_1P}_2, \overrightarrow{P_2P}_3,... \overrightarrow{P_n P}_{n+1}$, each vector starting at the endpoint of the previous vector.)
 |
 |
 |
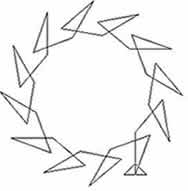
In the first diagram the lengths of the line segments are
equal and the angles of turn vary periodically in sequences of
length 3. In the second diagram the lengths of the line segments
vary periodically in sequences of length 5 and the angles of turn
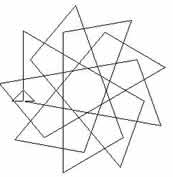
are equal. In the third diagram both the lengths and the angles
vary.
Investigate these patterns, give sequences of instructions
which would produce similar paths and explain why in each case the
spirolateral paths are closed producing a cyclic pattern when the
sequence is repeated infinitely often.
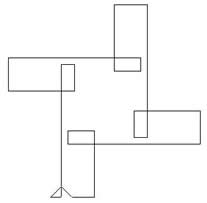
| Why does the spirolateral in this diagram continue indefinitely, shooting off to infinity if the sequence is repeated infinitely often? |