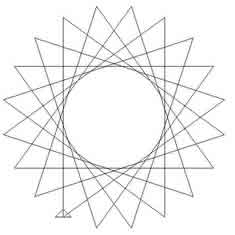To produce this star, twenty line segments of equal length are drawn in a continuous path, with equal angles between consecutive line segments. Imagine instructing a small creature to walk along the path. You would give the instruction to walk forward a certain distance then to turn through a certain angle and to repeat the instruction over and over again. To do this, you could use the Logo commands: repeat 20 [forward 100 right $\theta$]

Experiment with the Logo program
repeat $q$ [forward 100 right $\theta$]

What shapes can you draw? Vary $q$ and $\theta$. For what values of $\theta$ can you find closed paths (returning to the starting point)?

Prove that the path is closed if and only if $\theta$ is a rational multiple of 360 degrees.

Compare this property to the results found in the problem Stars.