Odd Differences

'Odd Differences' printed from https://nrich.maths.org/

Show menu

Tom started us off with the following idea. Thanks Tom.

In the square of dots you can imagine the"L" of any odd number and if you take the square for the odd number below it from the square of the odd number you get the number you stated with. To find the two squares you have to find half the odd number and round it up and down. So half of $13$ is $6.5$ so the two squares have sides $7$ and $6$.

Here is a picture:

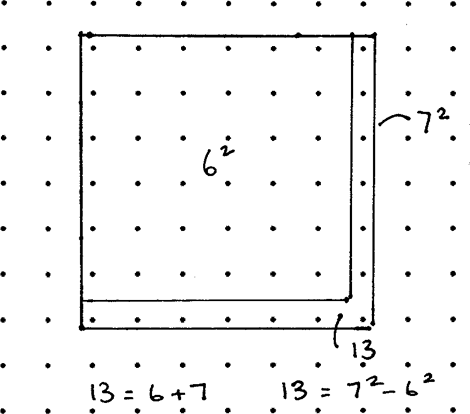
So, using the diagram you know that $$105= \frac{105-1}{2} + \frac{105+1}{2}$$

$$ 105 = 52 +53$$

$$ 105 = 53^2 - 52^2$$

You can always find one way using this method. So

$$1155= \frac{1155-1}{2} + \frac{1155+1}{2}$$

$$ 1155 = 577+578$$

$$ 105 = 578^2 - 577^2$$

Alex, from the Grammar School at Leeds extends the algebra building on the second visualisation:

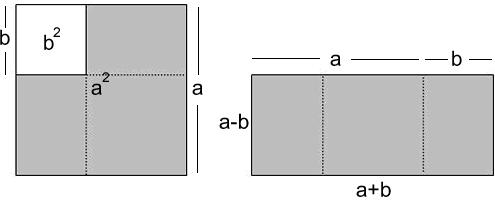
The task is to find eight pairs of numbers $(a,b)$, satisfying the following equation: $$a^2 + b^2 =115$$

The LHS can be factorized to $(a+b)(a-b)$, so now we can begin to find eight factor pairs of $1155$:

Using prime factorization,

$155 = 5 \times 231 = 5 \times7\times33 = 5 \times7 \times3 \times11$

Now we use different selections of these prime factors to build the list of eight factor pairs:

\begin{eqnarray} 1155 &=& 5 \times231 \\ &=& 7 \times165 \\ &=& 3 \times385 \\ &=&35 \times33 \\ &=&21 \times55 \\ &=& 15 \times77 \\ &=&11 \times105 \\ &=&1\times 115\end{eqnarray}

Then it is simply a matter of substituting each pair into the following procedure:

$1155 = (a+b)(a-b) = $ Large factor $\times $ small factor

$a + b =$ large factor

$a - b =$ small factor

$2b =$ large factor$-$ small factor

$b =$ (large $-$small)/$2$

$a = b + $small factor

Applying this to each pair: \begin{eqnarray} 1155 &=& 46^2 - 31^2 \\ &=&58^2- 47^2 \\ &=& 578^2 -577^2 \\ &=&118^2 - 113^2 \\ &=&86^2 - 79^2 \\ &=&194^2 - 191^2 \\ &=&34^2 - 1^2 \\ &=&38^2- 17^2\end{eqnarray}