Odd Differences

'Odd Differences' printed from https://nrich.maths.org/

Show menu

Why do this problem :

This connection between the set of odd numbers and squares is not often encountered in school and offers a very accessible example of visualisation.

The 'difference of two squares' is a key algebraic transformation and problems like this can lead students into a deeper appreciation of that form through a further visualisation.

Possible approach :

Start by giving learners time to make sense of the idea that any odd number can be written as the difference of two squares using the dotty grid. Encourage them to investigate with small numbers (for example, $9=5^2 - 4^2$ ) before generalising for larger numbers such as $1155$ and then devising a general rule for anyone to apply.

Remind them of the identity $a^2 - b^2 = (a + b)(a -b)$ and give them time to consider and see the connection with what they have already done. For example: $$9=5^2 - 4^2 = (5+4)(5-4).$$

At this point another visualisation might be useful in order to suggest how further differences might be found.

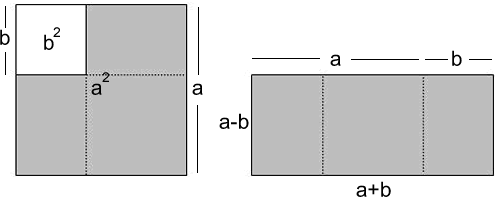
The problem of writing the number $105$ as the difference of two squares becomes a problem about factor pairs that make a product of $105$.

Draw out from the students how this transformation helps [we now seek factors of $105$ rather than guessing squares and calculating differences].

Moving to the last part, and even pushing beyond that to a general result, may require the group to spend time making sure that they are secure with an algorithm for producing prime factors.

Key questions :

Explain how this image shows us the sum of the first n odd numbers - what is that sum ?
For $105$ (and then for $1155$) how many ways might there be, and why do you think that ?

Possible extension :

Is it true that no number can be written as the difference of $2$ squares in exactly three ways, and if so why?

Possible support :

Perhaps try the problem Plus Minus first.

For students not yet ready for this problem, time spent on finding factors will be valuable. When the group are ready, check that they can use an algorithm to find prime factors and invite them to suggest how they can use that to assist factor-finding.