Take a line segment of length 1. We'll call it $C_1$.

Now remove the middle third. Call what's left $C_2$.

Now remove the middle third of each line segment in $C_2$. Call what's left $C_3$.

We can keep doing this, at each stage removing the middle third of each of the line segments in $C_n$ to form $C_{n+1}$.

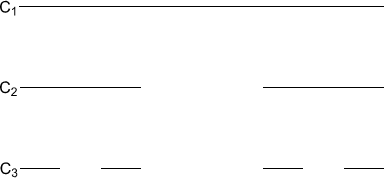
Draw pictures of $C_4$ and $C_5$.

If we suppose that the end points of $C_1$ are 0 and 1, then we can mark on the end points of the line segments for the later $C_n$ too. For example, $C_2$ has end points $0$, $\frac{1}{3}$, $\frac{2}{3}$ and $1$ as shown below.
Draw $C_3$ and label the end points, and label the end points on your pictures of $C_4$ and $C_5$.

We can keep removing middle thirds infinitely many times. The set of points left having done it infinitely many times is called the Cantor set.

Which of the following points are in the Cantor set?

$\frac{1}{3}$, $\frac{4}{9}$, $\frac{3}{81}$, $\frac{4}{81}$.

Explain how you decided which belong and which don't.

 

See also the problem Smaller and Smaller.