In this question, each of the letters $I$, $R$, $S$ and $T$ represents a different transformation.

We can do one transformation followed by another. For example, $R S$ means ``do $R$, then $S$''.

We can also undo transformations. For example, $R^{-1}$ means ``do the inverse (opposite) of $R$''.

Here are the effects of some transformations on a shape. Can you describe the transformations $I$, $R$, $S$ and $T$?
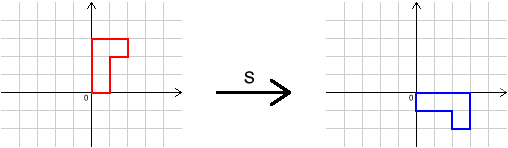
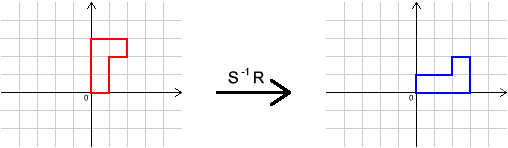
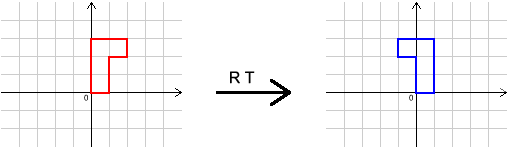
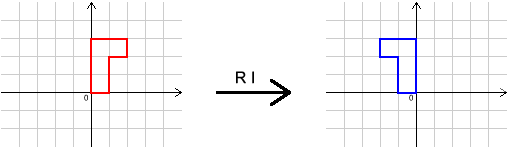
What single transformation has the same effect as $R S T I R^{-1}S^{-1}T^{-1}I^{-1}$?

This problem is the first of three related problems.
The follow-up problems are Combining Transformations and Simplifying Transformations .