Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
No Right Angle Here
Age 14 to 16
Challenge Level 





- Problem
- Student Solutions
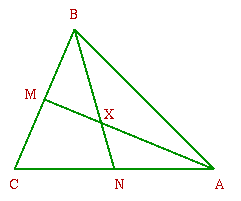
This is the solution by Tim from Gravesend Grammar School.
Assume that two of the internal angle bisectors, $AM$ and $BN$, are perpendicular to each other, meeting at $X$, ie $\angle AXB = 90^\circ$.
In triangle $\Delta AXB$, $\angle AXB + \angle BAX + \angle XBA = 180^\circ$
so $\angle BAX + \angle XBA = 90^\circ$.
But $\angle XAC = \angle XAB$ and $\angle ABX = \angle XBC$
so the sum of the angles in the triangle is $2 ( \angle BAX + \angle XBA ) + \angle BCA = 180^\circ + \angle BCA$
so $\angle BCA = 0$, so $ABC$ is not a triangle as it only has two angles,
hence $AM$ and $BN$ are not perpendicular.
Note: What is happening here is that $BC$ is parallel to $AC$.