Well done to Nishad from Thomas Estley Community College in England, who sent in this full solution to the main problem:

Firstly we get that the equations are:

$ab+c=2$
$ac+b=2$
$bc+a=2$

Now notice that $$(ba+c)-(bc+a)=2-2 \Rightarrow b(a-c)-(a-c)=0 \Rightarrow (b-1)(a-c)=0$$
This gives us 2 cases namely $b=1$ or $a=c$

Case 1: $b=1$

We can substitute this into the original equations that we had 
$a+c=2 \Rightarrow c=2-a$
$ac=1$
Hence
$a(2-a)=1 \Rightarrow 0=a^2 -2a +1 = (a-1)^2$

This gives us the solutions $a=1$,$c=1$

Hence 1 set of solutions $(a,b,c)$ is 
$(1,1,1)$

Case 2: $a=c$

We can substitute this into the original equations that we had 
$ab+a=2 \Rightarrow b=\frac{2}{a}-1$
$a^2+b=2$
Hence
$a^2 + \frac{2}{a}-1 = 2 \Rightarrow a^{3} - 3a +2 = 0$

Since $a=1$ is a root of the equation $(a-1)$ is a factor

$a^3 -3a +2 = (a-1)(a^2+a-2) = (a-1)(a-1)(a+2) = 0$

Using $a=1$ gives us the same set of solutions as before but $a=-2$ gives us a new set, namely 
$(-2,-2,-2)$

Nayanika from The Tiffin Girls' School in the UK began the first part of the extension:

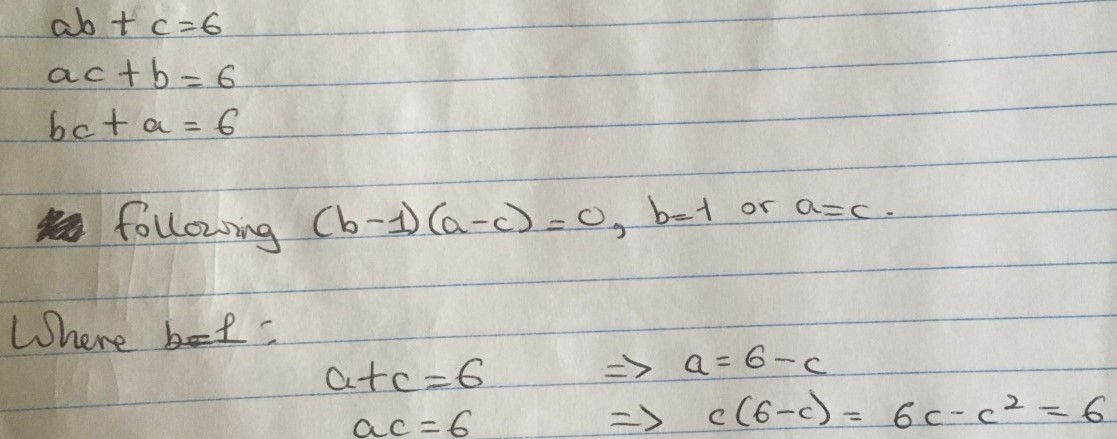
Here, it should say $ac+1=6,$ so $c(6-c) +1 = 6c-c^2+1=6,$ therefore $c^2-6c+5=0.$ From here, Clare continued:

$c^2-6c+5=0\Rightarrow (c-1)(c-5)=0$ so $c=1$ or $c=5.$
$a+c=6,$ so $a$ is the other out of $1$ and $5.$
This means $a,b,c$ are $1,1,5$ (in any order).

Case 2 - $a=c$
Now $ab+a=6$ and $a^2+b=6,$ so $b=6-a^2$
Therefore $a(6-a^2)+a=6\Rightarrow 6a-a^3+a=6 \Rightarrow a^3-7a+6=0$
We can see that $a=1$ is a solution (and this is not a surprise because we already know $b$ could be $5$ and $a$ and $c$ could both be $1$), so $a-1$ will be a factor:
$a^3-7a+6=(a-1)(a^2+a-6)=(a-1)(a+3)(a-2)=0$
Therefore $a=c$ could also be $-3$ or $2.$

If $a=c=-3,$ then $ac+b=6$ becomes $9+b=6$ so $b=-3$ as well. This will clearly work for all of the equations.
If $a=c=2,$ then $ac+b=6$ becomes $2+b=6$ so $b=2$ as well.

Therefore $a,b,c$ could be $1,1,5$ or $2,2,2$ or $-3,-3,-3.$

For the second part of the extension, Mattia wrote:

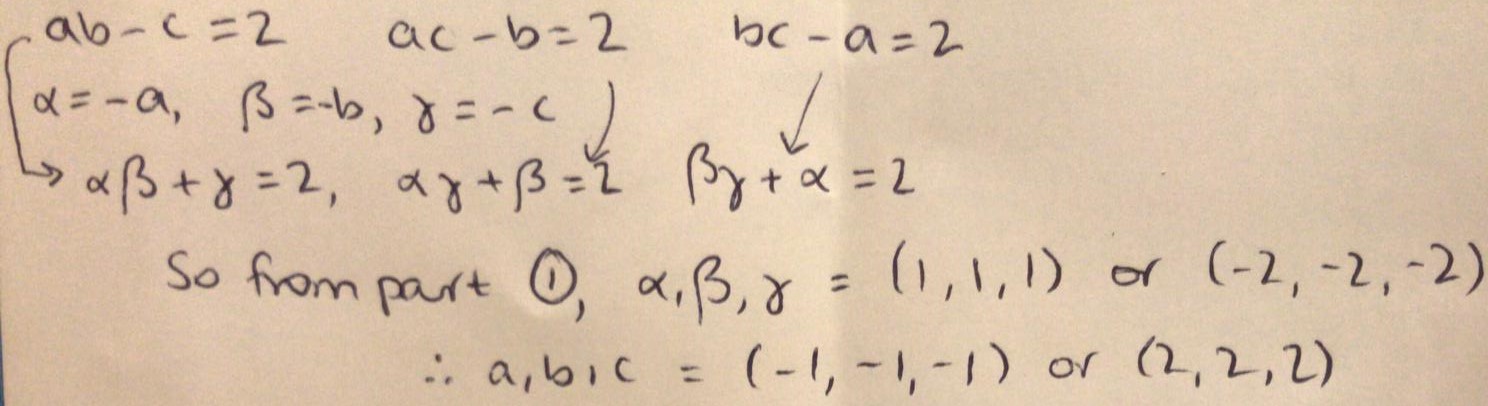
Nishad completed the extension by beginning with the further extension:

$ab+c=k$
$ac+b=k$
$bc+a=k$

Now notice that 
$(ba+c)-(bc+a)=k-k \Rightarrow b(a-c)-(a-c)=0 \Rightarrow (b-1)(a-c)=0$ so we get the same equation in the general case

Case 1: $b=1$

We can substitute this into the original equations that we had 
$a+c=k \Rightarrow c=k-a$
$ac=k-1$
Hence
$a(k-a)=k-1 \Rightarrow 0=a^2 -ka +k-1 = (a-1)(a-(k-1))$

This gives us the solutions $a=1$, $c=k-1$ (and $a=k-1$,$c=1$)

Hence 1 set of solutions $(a,b,c)$ is 
$(1,1,(k-1))$
but due to the symmetry of the problem all 3 permutations of this set are solutions, namely $((k-1),1,1)$, $(1,(k-1),1)$ as well.

Case 2: $a=c$

We can substitute this into the original equations that we had 
$ab+a=k \Rightarrow b=\frac{k}{a}-1$
$a^2+b=k$
Hence
$a^2 + \frac{k}{a}-1 = k \Rightarrow a^3 - (k+1)a +k = 0$

Since $a=1$ is a root of the equation $(a-1)$ is a factor
$a^3 -(k+1)a +k = (a-1)(a^2+a-k) = (a-1)(a-\phi)(a+(\phi+1)) = 0$ for some $\phi,$ where
$\phi (\phi +1) =k \Rightarrow \phi^2+\phi-k$
$\phi = \frac{-1+\sqrt{4k+1}}{2}$
$-(\phi +1) = \frac{-1-\sqrt{4k+1}}{2}$

Now we have new 2 new sets of solutions

When $a=\frac{-1+\sqrt{4k+1}}{2}$ gives us the set of solutions $$\left(
\frac{-1+\sqrt{4k+1}}{2},\frac{-1+\sqrt{4k+1}}{2},\frac{-1+\sqrt{4k+1}}{2}
\right)$$

When $a=\frac{-1 -\sqrt{4k+1}}{2}$ gives us the set of solutions 
$$\left(
\frac{-1-\sqrt{4k+1}}{2},\frac{-1-\sqrt{4k+1}}{2},\frac{-1-\sqrt{4k+1}}{2}
\right)$$

Remark: To find $b$ we could substitute the value of $a$ into 
$b=\frac{k}{a} - 1$
For the case where $a=\frac{-1+\sqrt{4k+1}}{2}$:
$$\begin{split}b&= \frac{2k}{-1+\sqrt{4k+1}} -1\\
&=\frac{2k+1-\sqrt{4k+1}}{-1+\sqrt{4k+1}}\\&=\frac{2k+1-\sqrt{4k+1}}{-1+\sqrt{4k+1}} \times
\frac{1+\sqrt{4k+1}}{1+\sqrt{4k+1}}\\ &=
\frac{2k+1-\sqrt{4k+1}+(2k+1)\sqrt{4k+1} -4k-1}{4k+1-1}\\&=\frac{-2k-\sqrt{4k+1}+(2k+1)\sqrt{4k+1}}{4k}\\& =\frac{-2k+2k\sqrt{4k+1}}{4k}\\& = \frac{-1+\sqrt{4k+1}}{2} \\&= a\end{split}$$
Which is why in fact $a=b=c$ (A very similar rationalizing of the denominator works for the case where $a=\frac{-1-\sqrt{4k+1}}{2}$) 

Extension 1:

After having done the further extension for the general case we can substitute in $k=6$ to get the sets $(5,1,1)$ (and its permutations), $(2,2,2)$, $(-3,-3,-3)$

Extension 2:

$ab-c=2$
$ac-b=2$
$bc-a=2$

Now notice that 
$(ba-c)-(bc-a)=2-2 \Rightarrow b(a-c)+(a-c)=0 \Rightarrow (b+1)(a-c)=0$

This gives us 2 cases namely $b=-1$ or $a=c$

Case 1: $b=-1$

We can substitute this into the original equations that we had 
$-a-c=2 \Rightarrow c=-2-a$
$ac=1$
Hence
$a(-2-a)=1 \Rightarrow 0=a^2 +2a +1 = (a+1)^2$

This gives us the solutions $a=-1$, $c=-1$

Hence 1 set of solutions $(a,b,c)$ is 
$(-1,-1,-1)$

Case 2: $a=c$

We can substitute this into the original equations that we had 
$ab-a=2 \Rightarrow b=\frac{2}{a}+1$
$a^2-b=2$
Hence
$a^2 - \frac{2}{a}-1 = 2 \Rightarrow a^{3} - 3a -2 = 0$

Since $a=-1$ is a root of the equation $(a+1)$ is a factor

$a^3 -3a -2 = (a+1)(a^2-a-2) = (a+1)(a+1)(a+2) = 0$

Using $a=-1$ gives us the same set of solutions as before but $a=2$ gives
us a new set, namely $(2,2,2)$