Here is a picture of the five Platonic solids:

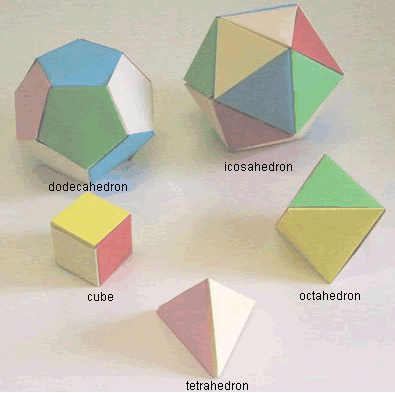
Imagine you want to make each of the five Platonic solids and colour the faces so that, in every case, no two faces which meet along an edge have the same colour.

Can you find the least number of colours for which this is possible for each polyhedron.

How did you go about finding your solutions?

If you'd like to make these solids out of paper, have a look at Ian Short's article.