We had lots of solutions to this problem but not many of you told us how you got your solutions. Luis and Freddie, who go to Newton Prep, sent in well-explained solutions. Here is what Luis wrote:

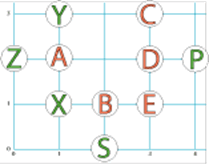
The first thing I worked out is that the letter at (4,2) is not symmetrical in any way, the only letter that isn't symmetrical in any way is the letter P.
Then I worked out that at (0,2) and (1,2) are the ends of the alphabet and had to be A and Z but I needed to know which one went where so I looked at the clues. One said that (0,2) and (2,0) have rotational symmetry which means that A is on (1,2) and Z is on (0,2).
Then I saw the clue that said that (3,3), (3,2) and (3,1) are all consecutive in the alphabet, because the A and the Z are already used, it has to be C, D and E because it says that (3,3) is made of only curved lines.
Then I saw that one of the clues said that (2,0) is only made of curved lines, so (2,0) is the S.
(4,2) is not symmetrical in any way so (4,2) is a P.
The first clue says that (1,1) and (1,3) have a vertical line of symmetry, another clue says that (1,1) also has a vertical line of symmetry, which means that (1,1) is a X and (1,3) is a Y, which leaves the B which is at (2,1) because a clue says that at (2,1) there is a letter with a horizontal line of symmetry.  

Many children from Stradbroke Primary School sent an image of their solution. Here is George's:

Well done!

Rose and Thomas from Minterne Junior School wrote the following

We know that (1,1) = X because it has both horizontal and vertical symmetry.
A had to be (1,2) becuase it has vertical symmetry and is at one end of the alphabet. 
Y was placed at (1,3) because it has vertical symmetry. 
We knew that X, S and Z have rotational symmetry, but X has to be at (1,1), so Z was placed at (0,2) because it is also at the other end of the alphabet, and S at (2,0) becuase it has
curved lines.
We put C (3,3), D (3,2) and E at (3,1) because they are consecutive.
This works because C at (3,3) also had to consist of curved lines, and E (3,1) had
to have just straight lines.
Finally, we put B on (2,1) becuase it has horizontal symmetry, and P at (4,2) becuase it has no lines of symmetry.

We had the following solution come in from Writtle Junior School in Essex. Reggie, Esther and Emily want to share this:-


“I first worked out that [0,2] and [1,2] are A and Z but I needed to work what goes where , I saw [1,2] had vertical symmetry so [1,2]  is A so [0,2] is Z. P is not symmetrical in any way so [4,2] is P, S is the only one left with rotational symmetry and Z has taken [0,2] so S is [2,0]. [1,1] is symmetrical horizontally and vertically and X is both so [1,1] is X. Y is left with [1,3] because it is symmetrical vertically and none else are left symmetrical vertically so Y is [1,3]. E Is left with straight lines so E is [3,1]. E is at [3,1] and [3,1], [3,2] and [3,3] are consecutive in the alphabet so [3,2] is D and [3,3] is C. [2,1] is left and B is left [also horizontal like the clue] must be at [2,1].”

Well done,all of you  for giving such clear descriptions as to how you came to your answer.